1954 Geometria 054

v

a z toho

(1)

AD

AE

u

I)alej su na obr. 67 zostrojene trojuholniky EDB a EDG. Maju spo-locnu stranu DE a k nej prisluśne vyśky su zhodne, lebo <£ A DE = = <£.A'B'C = <X ABC, a preto DE || BC. 0 obsahoch tychto troj-uhołnikov plati

(2)    A DEB = A DEC.

Ak poużijeme rovnost (2), dostaneme: (3) A ABE = A ADE + A DEB = A ADE + A DEC = A ADC. Ak yyjadrime obsahy trojuholnikov ABE, ADC, dostaneme:

A ADC = \r AC. v. £

A ABE = ~ AB.u Podia vztahu (3) je teda

	~ AB . u = ]-AC.v 2 2
cize (4)	AB v
	AG u
Spojenim rornosti (1) a	(4) dostaneme
	AB AD AC ~ AE’
ciże	AD AE AB ~ AC’

ale — = k, a preto je AE = k.AC, co sme mali dokazaf.

AB

Poznamka. Veta 2, ako. sami dalej poznate, je zakładom cełej nauky o podobnosti. Je obdobnou vetou ako veta usu 0 zhodnosti trojuholnikov. Zavedieme pre nu skratku uu a budeine ju nazyvat vetou uu o podobnosti trojuhołnikov.

Priklad 6 (obr. 68). Na jedno rameno duteho nhla s vrcholorn V nanesieme usećky vel’kosti a, b, krajne body oznaćime P, Q. Na druhe rameno tolio isteho nhla nanesieme usecku vel’kosti c, krajny bod oznaćime R. Bodom Q vedieme rovno-beźkn s priamkou PR a jej priesecik s pol-priamkou VR oznaci-me S. Mamę dokazat, że płat i

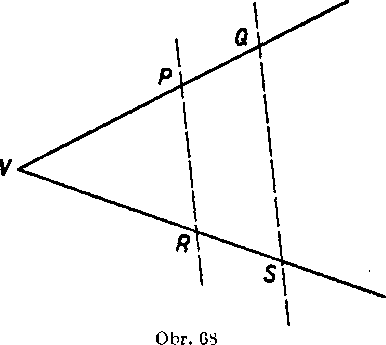
bc

IN

Rieśenie. Podia znaroej vety z 8. roe-nika je <c VPR — A A VQS. Podia vety uu je

A VPR ~ A P£S.

Z toho vyplyva

VR c

VS = k.VQ = k.b, VR = k. VP, ćiże k = ~ po dosadeni dostaneme vzfah (6).

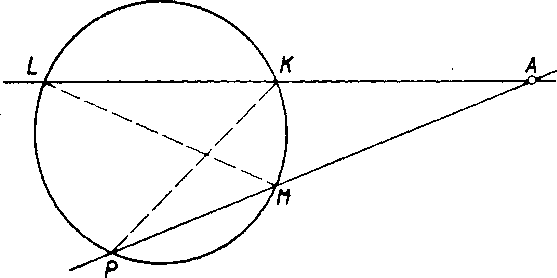
Obr. 69

Tento vysledok poużivame ćasto pri różnych konstrukcjach (pozri cvicenie 6).

55