1954 Geometria 316

18. Kolko m³ śtrku jo na hromade tvaru patstena z obr. 68, ktoreho podstava je obdlźnik a vzdy dve protilahle bocne steny maju od roviny podstavy rovnaku odchylku, ak a_x = 3,5 m, a₃ = 2,8 m, a₂ = 1,2 m a■ v = — 0,9 m.

y^. Kol’ko m³ obsahuje pójd (tvaru patstena z obr. 68; ktoreho podstava je obdlźnik a vźdy dve protilahle bocne steny maju od roviny podstavy rovnaku odchylku) nad obdlźnikom = 18,5 m, a₂ = 10,5 m, v = 3,6 m; aka je dlżka «₃ hrebeńa'?

Urcte vel’kost uźitkoveho priestoru, ak sa tento rovna 85% priestoru pokryteho stre-chou.

20.    Jama ma tvar pravide!nehośtvorbokeho zre-zaneho ihlana. Hrany podstav su a_t = 1 m, a₂ — 10 m; bocne steny maju spad 1:1.

a)    kolko m³ zeme sa vykopalo ?

b)    kolko m³ betonu pribliźne treba na vy-betónovanie jamy, ak ma byt hrubka betonu 1 dm? IMa hruby vypocet pouźite piast telesa.

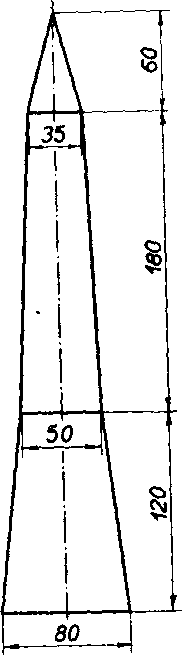
21.    2ulovy pamatnlk (obr. 69; rozmery su v centimetroch) sa składa z pravidelnych śtvorbokj'ch ihlanov, a toz dvoch zrezanych a jedneho uplneho. Urcte jeho vahu (spec. vaha źuly je 2,8 gem³).

22.    Kolko m³ riećneho piesku je na hromade pravidelneho §tvorbokeho zrezaneho ihlana s podstavnymi hranami a_x = 5,5 m, a₂ =

Obr. 69    = 4,5 m a vyśkou v = 1,2 m?

5. Objem rotacneho valea a kuźela

Pre objem rotacneho vałca platl veta obdobna vete 1, ktoru sme wiedli pre hranoly:

Yeta 5. Objem rotacneho valca sa rovna sucinu obsahu podstavy a Yelkosti vysky.

Dókaz.

Nech ma dany rotacny valec podstavu o obsahu p, vel’kost vyśky valca oznacme v. Ak je V jeho objem, marne ukazat, źe plati V = pv. Preto poroynajme dany valec s opisanymi a ypisanymi hranolmi. Pritom pod opisanym hranolom rozumienie koimy hranol, ktoreho podstava je yypukly mnohouholnik opisany podstave daneho valca; jeho bocne steny sa dotykaju valca, vyska sa rovna vyske daneho valca. Obdobne pod ypisanym hranolom rozumieme koimy hranol, ktoreho podstava je yypukly mnohouholnik ypisany podstaye daneho valca a jeho strany sri stranami valca; yyska sa rovna vyśke valca.

Je zrejme, że valec je castou każdeho opisaneho hranola (a je od neho różny) a dalej, że każdy ypisany hranol je castou valca (a je od neho różny). Móżeme teda poużit vetu z poznamky 3: ak oznacime V objem vpisaneho hranola a V" objem opisaneho hranola, plati

V'< V < V".    (1)

Ak dalej oznacime p' (p") obsah podstavy rpisaneho (opisaneho) hranola, móżeme pisat V' = p'v, V" = p"v, a teda posledna nerovnomer-nost (1) dostane tvar

p'v < V < p"v.

Zvol’me teraz postupnost pravidelnych vpisanych hranolov tak, aby każdy hranol postupnosti mai dvojnasobny pocet vrcholov, neż ma prave predośly hranol postupnosti. Tym je sucasne dana postup-nosfi obsahov p' ich podstay, o której vsak vieme, że ma za limit obsah p podstavy yalca; teda postupnost, ktoru dostaneme, ked’ każdy obsah p' predoślej postupnosti nasobime yyskou ypisanych hranolov, t. j. postupnost ich objemov ma za limit sucin pv.

Obdobne vol’me postupnost pravidełnych opisanych hranolov vy-hovujucich podmienke, aby każdy hranol postupnosti mai dvojna-sobny pocet yrcholoy, neż ma hranol, który mu v postupnosti bez-prostredne predchadza. Tym je opat dana postupnost ich podstav, a teda aj postupnost ich obsahoy p"; o tej to postupnosti vśak vieme, że ma za limit tak isto obsah podstavy yalca. Postupnost tvorena clenmi p” predchadzajucej postupnosti obsahoy podstay opisanych hranolov nasobenymi yyskou v hranolov, teda postupnost objemov zostrenych opisanych hranoloy, ma za limit tak isto ćislo pv.

Ak objem w-teho (m-teho) hranola naśej postupnosti ypisanych (opisanych) hranoloy oznacime Vń {V'ń), potom podia (1) dostaneme nerovnosti

f;< v, v< f;'_;

317