1954 Geometria 160

vzajomnu połohu 3, bud 4 (każde dve z nich su róznobeżne a je r |j .s). Preto je r || q.a, t. j. aj p || g.a.

Priklad 9. (obr. 20.) Je dany kvader ABCDA'B'C'D' v zakladnej polohe. I)alej je dany bod U, który leżi vo vnutri hrany AB, V je bod leżiaci vo vnutri hrany BO. Vo vol’nej projekcii mamę zostrojit priesek kvadra s rovinou XJVD'.

Rieśenie. Prieseenica roviny o = UVD' s rovinou ABC je priam-ka W. Priesecikom Q priamok U V, AD prechadza prieseenica rovin

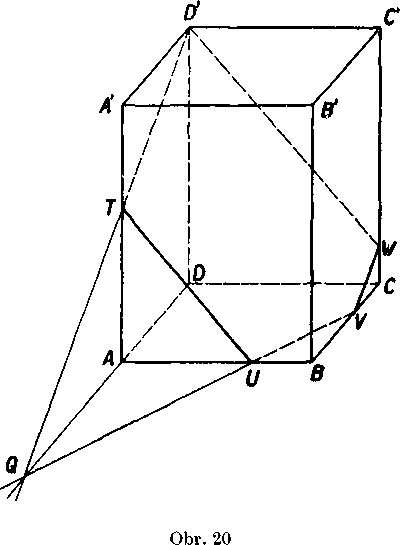
q, ADD', lebo bod Q je spolocny bod rovm o, ABC, ADD'. Priamka QD' je prieseenica rovin q, ADD'. Prieseenica rovin o, BCC' je podia vety 3 (pripad 2) rovnobeżna s priamkou QD a prechadza bodom V. Z obdobneho dóvodu je aj prieseenica rovin o, CDD' rovnobeżna s priesećnicou roAdn p, ABB' a prechadza bodom D'. Tak zostrojime priesecny pafuholnik D'TUVW.

Cvicenie

1.    Priamka p je rovnobeżna s rovinou q a q je l’ubovoIna priamka tej to roviny. Aka móźe byt vzajomna poloha priamok p a q?

2.    Su dane dve mimobeźky, p, q a bod A. Dokaźte, że existuje jedina rovina bodom A rovnobeżna s p aj q.

3.    Priamka je urcena smerom a bodom. Dokaźte to.

4.    Dane su dve mimobeźky p, q a bod A, który neleżi ani na jednej z nich. Dokaźte, że bodom A prechadza najviac jedna priecka mi-mobeżiek p, q. Navod: postupujte ako v priklade 7.

5.    Priamky a, b, c pretinaju danu priamku m; pritom plati a \\b, b |] c. Dokaźte, że priamky a, b, c, m leżia v jednej rovine.

6.    Nech a, m nie su rovnobeżky. Dokaźte, że priamky smeru a, pre-tinajuce priamku m, vyplńuju rovinu.

7.    Ak sujaff dve roviny, dokaźte, że v jednej z nich existuje neko-necne mnoho priamok rovnobeżnych s druhou. Co o nich móżete povedat, ak nie je o [| ar?

IL Preco je vo vete 9 podmienka, że obe priamky musia byt róznobeżne ?

u. Ako sa zisfuje trubkovou libelou, że nejaky rovinny obrazec je vodorovny? Odóvodnite geometricky.

10.    Rozhodnite o spravnosti alebo nespravnosti nasledujucich usud-kov a odóvodnite svoje tvrdenie (p, q, r su priamky, o, a, z su roviny):

ak je p\\q, q ||r, je p ||r;    0!)    ak    je q j| a, a || r, je ą || r.

O) ak jep || q, q j) q, je p ]] q; O) ak je p || q, q || a, je p || a.

§) akjep || q, q \\q, je p ||g; (§) ak je q || p, p || a, je q || a.

gfy ak je priamka p róznobeżna s rovinou q a rovina o rovnobeżna s rovinou a, je priamka p róznobeżna s rovinou a\ h) ak je priamka p rovnobeżna s priamkou q a priamka q róznobeżna s rovinou q, je priamka p róznobeżna s rovinou o.

11.    Nech je dana rovina q a v nej róznobeżnik ABCD. Nech je dalej dana priamka a, która prechadza bodom A, ale neleżi v rovine q a dalsia priamka c\\a, która prechadza bodom C. Dokaźte, że sa roviny Ba, Dc, ako aj roviny Ba, Da pretinaju v priamkach u, v, pricom je u || v || a.

12.    Dokaźte, że ak je priamka p rovnobeżna s dvoma navzajom rózno-beżnymi royinami q a a, je rovnobeżna s ich priesećnicou.

161