1954 Geometria 338

Veta 2. Ak poyrch telesa T je rozlożeny na dve neprckryyajuce sa: casti T_1; T₂, potom yelkosf poyrehu telesa T roynasuctu yelkostl casti Tl T₂.

Poznamka 1. Dve neprekryyajuce sa casti povrcłm telesa su take jełio casti, z których ani jedna neobsahuje vnutorne body druhej casti.

Poznamka 2. Vetu' 2 by sme mohli doplnit este dalśimi dvoma tvrdeniami: 1. ve!kosf povrchu je kladne cislo, 2. zhodne povrchy su rovnako velke.

Pórovnajte vetu 2 s tymito doplnkami a vlastnostami [1], [2], [3J pre obsahy (str. 270) a aj pre objemy (str. 295).

Poznamka 3. iJpinou indukciou by sme dokazali, że veta 2 plati aj pre IubovoIny poćet neprekryvajucich sa casti povrchu telesa.

2. Povrch hranola a ihlana

Nasa definicia ve!kosti povrchu telesa a jeho casti vedie v pripade-hranola k uż dobre znamej vete:

Yeta 3. Povrch hranola rovna sa suctu obsahoy jeho podstav a bornych stien.

Dokaż te sami. Poużite na to obidve vety z predchadzajuceho clanku.

Poznamka. Ak su napr. rozmery kvadra a, b, c a ked’ je P jeho> povrch, potom

P — 2(ab -f- 6c -f- ca).

Podobna veta plati aj pre ihlany:

Veta 4. Povrch ihlana rovna sa suctu obsahoy jeho podstayy a boc-nych stien.

Dokaż yynechame. Możno ho yykonaf pomocou vety 1 a 2 pred-dośleho clanku.

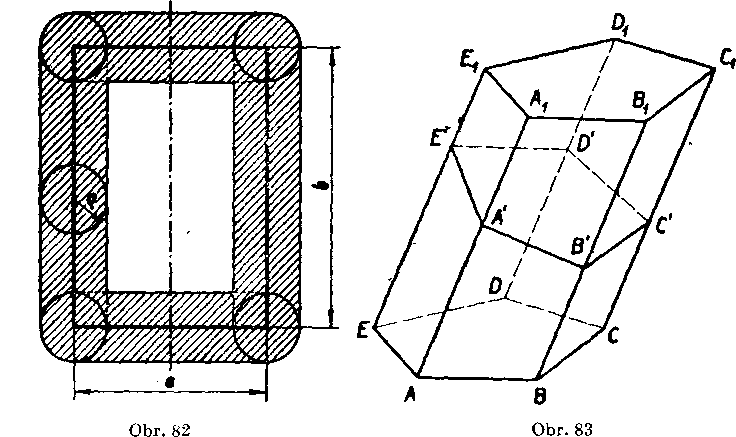
Priklad 1. Treba urcif yelkosf povrchu kvadra iha pomocou de-finicie z predchadzajuceho clanku.

Rieśenie: Teleso Tę zostrojene pre dost małe ę(urcte hranicu pre-q) k danemu kvadru T o rozmeroch a, b, c mcżno povażovaf za rozdiel dvoch telies T_Ł a T₂ (na obr. 82 je zobrazeny rez telesom Tę koimy na hraira c kvadra, T₂ je kvader o rozmeroch a — 2g, b — 2g, c — 2o; opiśte teleso Tj). Pretoże objem telesa T_x rovr>a sa

abc -f 2(a6 -j- ac -f bc)g + rc(a + b -f- c)g² + ~ 7ig^z

ó

a objem T₂ rovna sa

je

abc — 2(ab Ą- ac -f- bc)g -j- 4(ei -j- b -j- c)g² — 8g³, P„ =    = 2(ab + ac + bc) + M -f Bg²,

zg

kde A a B su koeficienty, które nezavisia od g; netreba ich bliżsie ur-covat. Z toho vidno, że povrch kvadra rovnń sa 2(ab + ac + bc) (pre vypocet limitu priradenej postupnosti P_ln poużite poznamku (na

Pre Yelkost piasta hranola a ihlana (namiesto ,,veIkost piasta“ budeme strućne hovorit len piast) plati:

Piast hranola (ihlana) rovna Sa suctu obsahov jeho bocnych stien. I)okazovat nebudeme; tvrdenie vety vyplyva z oboch predośłych viet.

339