1954 Geometria 346

Veta 7; Plasf rotafineho valca rovna sa sucinu obvodu podstavy a vel-kosti vysky.

Dokaż. Oznaćme polomer daneho valca r, jeho vyśku v. Zostrojme pre piast T daneho valca teleso T_s; ked zvolime kladne o mensie neź r, potom Tq je rotacne teleso, ktoreho osovy rez je zobrazeny na obr. 85

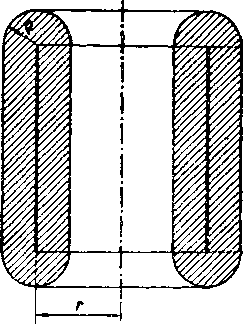
Obr. 86

(popiśte teleso). Jeho objem odhadne-me. Teleso' T_e zovrieme medzi dve telesa ^xT_e a ¹T_e; obidve sa lisia od tak, że T_e je castou telesa ²T_e a ¹T₀ je ćastou T_g.

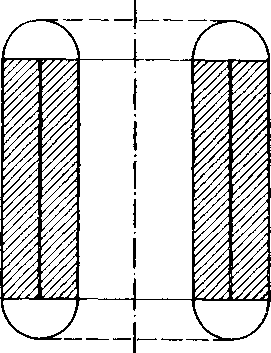
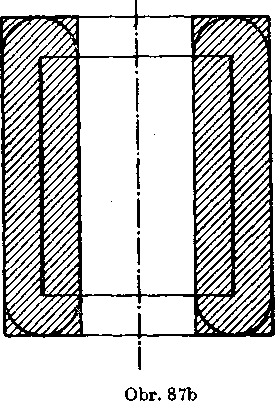
Za volime duty valec o vy§-ke v -j- 2p, o polomeroch podstav r -f- q, r — g (obr. 86) a za ¹T_e duty valec o vyske v a o polomeroch podstaw r + q, r — q (obr. 87).

Ked’ oznacime objemy telies ²T_? a ¹T_e pismenami ²F₉ a ¹F_e, plati podia pozn. 3 (cl. 1.) nerovnost

Poznamka 3. Pravouhly rovnobeżnlk, ktoreho strany su obvod podstavy valca a vyśka valca, nazyvame rozvinuty piast valca. Ked totiż rozreżeme piast vałca podia jeho strany, je zrejme, że platl: Piast valca możno rozvinut do roviny tak, że vznikne spomlnany rovnobeżnlk. Dóleżite je, że toto tvrdenie możno dokazat, ked’, prav-da, vopred presne yymedzime pojem rozvinutia; tymto sa vśak nebu-deme zaoberat.

Veta 8. PlaSf rotaenebo kużela rorań sa poUmfoiemu sucinu obvodu podstavy a strany.

Podrobne to dokazovat nebudeme, pretoże metóda dókazu je podobna ako v kapitole 3 a 4.

1.    Ak oznacime piast kużela, ktoreho polomer podstavy je r a vyska v, plsmenom p, móżeme obsah vety vyjadrit vzorcom

p = Jirs.

Ak P oznacime povrch uvedeneho kużela, je

P = nr{r + «).

2.    Kruhovy vysek, ktoreho polomer sa rovna strane kużela a prislu-chajuca dlżka obluka obvodu podstavy kużela (obr. 88, kde s znamena stranu kużela a r polomer jeho podstavy), vola sa rozvinuty piast kużela. Nazov możno odóyodnit podobne ako v poznamke 3 cl. 4.

347

1

F_e = 4 nrvQ.

Ked dosadime z (2) do (1) a vydelime ziskane nerovnosti 2q, dosta-neme pre P_f nerovnosti

2tirv + 4nrQ > P_g > 2rcrv;

z tobo podobnou uvahou ako v cl. 3 (str. 343) zistime, że piast valca rovna sa 2nrv.

Poznamka 1. Ked oznaóime piast valca o polomere r a o vyske v pismenom p, móżeme vyslovenu vetu vyjadrit vzorcom

p = 2jcrv.

Sućasne móżeme odvodit vzorec pre povrch valca; ked oznacime jeho povrch P, je

P = 2nr{r -Ą- v).

(Urobte podrobne!)

Poznamka 2. Ked si uvedomime, że strana rotacneho valca rovna sa jeho vyśke, móżeme vetu 1 pre piast vyslovit aj v tvare: Piast rotacneho valca rovna sa sucinu dlżky krużnice podstayy a strany.

2

F₄>F_e>¹F_e;    (1)

p = 2 nrv. ^xF_e a ¹F_e lahko urcime:

¹V_Q — 4nrvq -j- Snrg¹    (2)