1954 Geometria 096

V. YETY EUKLIDOYE, VETA PYTAGOROYA A ICH POUŹITIE

1. Odvodenie viet

Teraz poużijeme poznatky o podobnosti trojuholnikov na to, aby sme odvoćUIi tri dóleżitd vety o pravouhlom trojuholniku, które boli zname uż starovekym geometrom. Prve dve su tzv. vety Euklidove.

Aby sme mohli Eu-klidove vety strucnej-śie vyslovif, zavedieme novy nazov. Na obr.

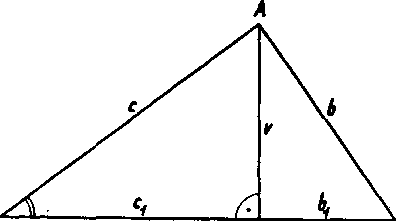
111 je pravouhly troj-uholiuk ABC a jeho yyśka AD. Ijsecky BD,

CZ> pomenujeme useky prepony, prilahle poradę k odyesnam AB,    __

AC.    B    a _D    C

Yeta 1. Ak je ayel-

kost prepony pravo-    Obr. iii

uhleho trojuholnika,

b, c Telkosti jeho odvesien, v yelkosf vy§ky a b_v c_x yelkosti prilahlych usekoy k odyesnam 6, c, plati

v² = 6₁c₁ (Eukłidoya veta o yySke);

b² = ab_v c² — ac_l (Eukłidoya veta o odyesne).

Ak uvażime, że v² je obsah stvorca o rozmere v a że b_x.c± je obsah obdlżnika o rozmeroch b_v c_v móżeme obidve Euklidove vety vyslovit takto:

Obsah śtvorca zostrojeneho nad yyskou pravouhleho trojuholnika rovna sa obsahu obdlżnika, zostrojendho z obidvoch usekoy prepony (veta o vyske).

Obsah stvorca zostrojeneho nad odvesnou pravouhleho trojuholnika rovna sa obsahu obdlżnika zostrojeneho z prepony a z prilahleho useku prepony (veta o odvesne).

Dókaz (obr. 111), 1. Pretoże ,ABD + BAD = 90° a <^CAD -j--f- A^BAD = 90°, je ABD = <3iCAD. Podia vety uu je

a preto

ciże

/\ABD ~ {\GAD,

v

b_x v ’ v² = b₁c₁.

2. Pretoże <$iABD = <f.ABC, je podia vety uu

a preto

ciże

A ABD ~ fcSJBA,

c_x    c

c    a ’

c² = ac_v

Obdobne sa dokaże, że b² = ab_v

Priklad 1. Obdlżnikma rozmery x, y (x < y). Marne zostrojit śtvorec toho isteho obsahu, aky ma dany obdlżnik.

Riesenie. Oznacime z vel’kost strany hladaneho śtvorca. Podia danej podmienky plati:

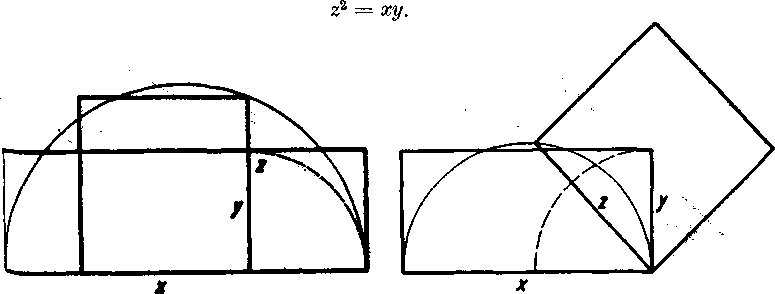
Obr. 112

Obr. 113

97