1954 Geometria 256

beżna s priesecnicou obidvoch rovin, potom że veta plati pre TubovoIny trojuhołnik a napokon, że plati pre każdy mnohouholnlk.

ra prechadza priamkou AB. Pravo-

uholnika [\ABC" oznaćime plsmenom p', je podia poznamky na za-ćiatku dókazu    ^v

1. Nech strana AB trojuholnlka ABC je rovnobeźna s priesecni-cou a s rovinami n, q (obr. 13). Potom je tato strana (vieme to zo stereometrie) rovnobeżna s rovinou n. Zostrojlme rovinu v 11 n, któ

p' = p.cosa.

Pretoże A A'B'G' je zaroven pravouhlym priemetom trojuholnlka l\ABC, prlpad 1 vety 4 sme dokazali.

2. Nech nie je nijaka strana trojuholnlka A ABC roynobeżna s prie-secnicou a s rovinami n, o (obr. 14). Tento pripad upravime na pre-dośly tym, że jednym z vrcholov (na obr. 14 vrcholom A) Yedieme priamku AX || a. Priamka AX leżi v rovine o a rozdęli trojuhołnik /\ABC na dva neprekryvajuce sa trojuholniky Ai> A2; które maju tu vlastnosfi, że jedna strana {AX) każdeho z nich je rovnobeżna s priesecnicou a rovin jt,, n. Ak sa obsahy trojuholnikov Ai> A2> P° poriadku rovnaju p_x, p₂, obsahy ich priemetov A’i> A’g ^sa opal po poriadku roynaju (podia ods. 1).

Pi = pj.cos», p₂ — Pi-cosa.

Obsah p' trojuholnlka AA’B’0' je

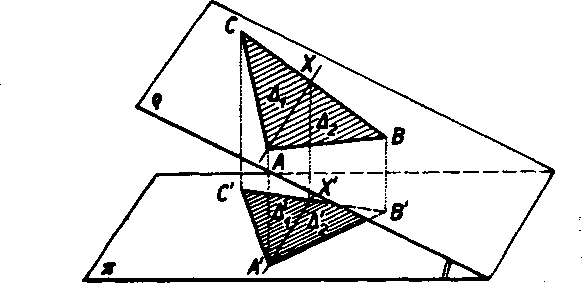
Obr. 14

p' = p[Ą- Pi = p_x- cos* -f- Pi • cos<% = (pi -f- p₂) cos«. Ćislo p_x + Pi nie je vśak nic ine ako obsah p trojuholnlka A ABC. Teda aj v tomto pripade

p’ = p. cos^y.

3. Nech v rovine o leżi IubovoIny mnohouholnik M o obsahu p. Jeho prayouhly priemet do roviny n oznaćime M'; obsah priemetu M' oznacime p’ (obr. 11).

Rozlożime mnohouholnik M na trojuholniky Ai> A₂>---> Ai> których obsahy su po poriadku p_x, p₂,,.., p_k. Pritom je, pravda,

p = Pi + Pi+ ... + p_fc.

Priemety trojuholnikov Ai> A2. • • •, A* su trojuholniky Ai> A₂ 3 ■ • • j Afc> których obsahy rovnaju sa po poriadku (podrą ods. 2)

257