1954 Geometria 312

Pretoźe obidve postupnosti maju ten isty limit, plati

lim!!E(₁ + —) (l + J-)

n->cQ 3 ^K ^ nⁿ ^ 2n

-- lim _J-U-l —    ^

n-^oo 3 n    2 n    3

Pretóże plati nerovnost (6), rovna saćislo Fspolocnemu limitu obi -dvocb postupnosti, musi sa teda F = — vp, cim sme vetu za pred-

O

pokładu, że P je bodom podstayy ihlana, dokazali.

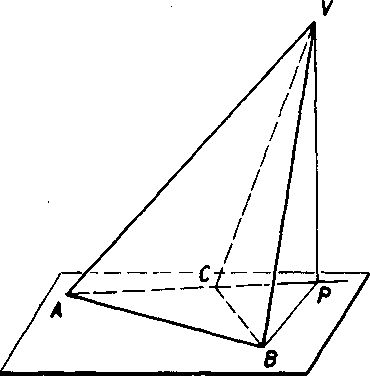
Obr. 66

Yetu treba dokazat este aj pre pripad, ked’ P nie je bodom podstayy daneho ihlana. Dókaz tejto ćasti nebudeme vysvet-l’ovat podrobne. TJkażerne len jeho metódu na najjednodueh-śom pripade.

Nech je dany trojboky ihlan ABCV (obr. 66) tak, aby pata P vysky vedena vreholom F na rovinu podstavy ABC bola mimo trojuholnika ABC-, pre jed-noduchost predpokladajme, że je bodom priamky AC. K danemu ihlanu ABCF pripojime dalsi ihlan CBPF; tym vznik-ne ihlan ABPV. Obidva maju uvedenu ylastnost. Pretoźe ihlan ABP V sa składa z dyoch yzajomne sa neprenikajucich ihlanor ABCF a BPCF, podia [3]objem ihlana ABCFrovna sa rozdielu objemoy ihlanoy ABPF a BCPF. Pre posledne dva ihlany móżeme poużit uż dokazanu vetu. Pretoźe vśak vśetky tri ihlany maju tu istu yysku a podstava daneho ihlana je rozdielom podstay zlożeneho a pripojeneho ihlana, plati dokazovana veta aj pre dany ihlan.

Poznamka. Ak oznaćime objem ihlana F, obsah jeho podstayy p a yysku v, potom tyrdenie vety je dane yzorcom

F = — pv.

Nakoniec ako aplikaciu pripojime ulohu:

iJloha 1. TJrcte objem zrezaneho ihlana.

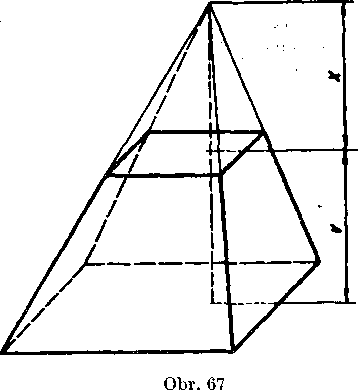
Riesenie. Nech obsahy podstay daneho zrezaneho ihlana su p_t, p₂, jeho yyska nech je v. Vieme, źe każdy zrezany ihlan móżeme pokładał za rozdiel dvoch ihlanoy, których podstayy su podstayy zrezaneho ihlana a pritom maju spolocny yrchol. Zostrojime tieto ihlany (obr. 67, kde je zvoleny stvorboky zrezany ihlan). Predpokladajme p_x > > p₂; ak sa vyśka ihlana s mensou podstavou rovna x, potom yyska druheho ihlana je v + x.

Ak oznacime F objem daneho zrezaneho ihlana, najdeme podia ylastnosti [3]

V = j p_x {v + *) — j ptfc = ||p_xv — PaS] (⁷)

Pre objem V móżeme vsak najst yyjadrenie len v prv-koch p_x, p₂ a v daneho zrezaneho ihlana.

Poużitim pomocnej vety,kto-ru sme dokazali na zaciatku tohto clanku, najdeme totiż pre yysku x

Pi ’■ Pi — (^v + ^x)² : *²> a teda

U '• fPa = (V + x) : x, z coho vyplyva (vzh!adom na to, że]Ap_x — 1/p₂ > 0)

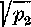
VPx — I/P2

Ak dosadime tento vyraz do (7), najdeme

V

fal — U

(VPi + Vp₂) móżeme predosly yy-

I „ „ , (Pi —PaMfo

₃ Pl® + u- u-

rozkładom p_x — p₂ = (jp_J —- j/p₂ sledok konecne uprayit na tvar

V

(Pi + IPiPz + Pi)’

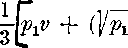
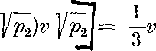
co je hladany yzorec pre ^ypoćet objemu zrezaneho ihlana.

313