1954 Geometria 202

vol’nu priamku v rovine q móżeme zrejme vziat priamku q precha-dzajucu bodom M, pretoże każda ina priamka r roviny q je rovnobeżna s jednou takou priamkou q vedenou bodom M a podia definicie plati

= < pq-

Oznaćme B patu kolmice, vedenej z bodu A na priamku q. VeIkost usecky AA₀ je vzdialenost bodu A od roviny q, a je teda AA₀ 5S AB (rovnost nastanę len vtedy, ked p₀ = q). Ak je B & M, potom z pra-vouhlyeh trojuhólnikov A A₀M a ABM so spoloćnou preponou AM vyplyva <£pp₀ = ^VQ ^ An- Ak je B = M, je <£    = 90°, <£ PQ< 90°,

vetu 30 celkom dokazali.

teda zase <£ PQ < pq• Tym sme

Obr. 53

Teraz konecne móżeme defino-vaf odchylku dvoch rovin.

Definicia. Odchyłka dvcch royin q a a je odchyłka priesecnic rovin q a a s Iubovol’nou rovinou r, pre ktoru plati r Jja r J_ a.

Je zrejme, że takto definovana odchyłka nie je zavisla od yol’by pomocnej roviny r.

Obdobne ako prv, budeme poużivat zapis A~Q^a P^re odchylku dvoch rovin; zrejme plati <£qg =    oq.

Ak je q || a, je <£ qo = 0, ak je q J_ <*> je <£ qa = 90°.

Bez dókazu uvedieme vetu, ktoru budeme ćasto poużivat pri zisto-vani odchylky dvoch rovin.

Veta31. Aksugau dve roviny, a a b dva smery take, że a J_ q, b J_ a, je qo = <£ ab (obr. 51).

V praxi sa casto meria skłon nejakej roviny, t. j. odchyłka tejto roviny od roviny vodorovnej. Ide napr. o meranie skłonu dopadovej roviny lyżiarskeho mostika, żeleznićnej tratę, nasypoy pri tejto trati, pola na svahu a pod. Merat sa może bud pomocou meracskej laty a li-bely (a uhlomeru), ako na obr. 52, bud osobitnym jednoduchym pri-strojom, tzv. svahomerom (obr. 53).

Pre vypocet odchylky dvoeh priamok, dvoch smerov, priamky (smeru) a roviny, droeh rovin móżeme zaviest goniometricke funkcie sinus, kosinus, tangens, kotangens ako obvykle, pretoże tieto funkcie su definovane pre ve!kosti uhla. Oproti rovinnej trigonometrii su pomery v priestore zjednodusene tym, że vśet^%y hodnoty funkcii su — pokial su definovane — cisla nezaporne.

Priklad 11. Je dana rovina n a v nej prumka p. Ved'te priamkou

I/3"

p rovinu a tak, aby bolo tg <f. na = Konstrukciu urobte na kocke ABGDA'B'G'D' v zakladnej polohe a vo!te o = ABGD,p = AG.

D'    C

N

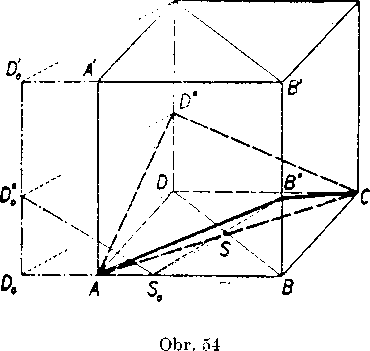
Riesenie(obr.54).Pre-toieAG ±_BD&AG \_BB', je te = DBB'D' pomocnou rovinou, pre ktoru plati n J_ P- V rovine n treba narysovat priamku q bodom 8 = AG.DB tak, aby <t qr = 30°, kde r = DB. Za tymto ućelom otocime obdlżn i k DBB' D' około strany BB' tak, aby jeho rovina splynula s ro-vinou ABB’A', która je rovnobeżna s nakresńou.

Nóva poloha obdlżnika budę D₀BB' D"₀ a bod 8 prejde do bodu S₀. (Bod D₀ najdeme zrejme tak, że nanesieme BD’ = Bf)’.)

Teraz narysujeme priamku q₀ bodom 8₀ (su dve riesenia) a dostaneme body B" na priamke BB' a Z>q na priamke D₀Dq. Po otoceni spaf su dve hladane roviny dane bodmi AB"G a AD"C. Na obrazku su za-kreslene aj prieseky t^chto rovin s kockou.

Priklad 12. V kvadri ABCDA'B'C'D' urcte odchylky telesovej uhlopriecky AC' so stenovymi uhloprieckami s ńou róznobeżnymi. (Je dane AB = a, BG — b, AA' = c.)

Rieśenie. Kvader ma 12 stenovych uhlopriećok, które su po dve roynobeżne. Telesova uhlopriecka AC ma teda so stenovymi uhlo-prieckami celkom 6 odchylok. Tri z nich su urćene uhloprieckami, które su s telesovou uhloprieckou ^46' róznobeżne.

203