1954 Geometria 126

body dotyku. Priamka t pretne priamku -S^i keby boii obe priamky roYnobeżne, vznikol by obdlżnik S₁T₁T₂8₂ a v nom by platilo = = 8₂T₂, ciże >\ = r₂, co je sporne s danymi ćislami t\, r₂. Oznaeme M priesecik priamok S_x8₂, t; rovno!ahlost so stredom M, która prevadza bod 8_X do bodu S₂, prevedie aj bod T_x do bodu T₂, a preto prevedie krużnicu l\ do kruźnice k₂.

Bod M je teda jeden zo stredov rovnol'ahlosti. Bod M vsak neleżi medzi bodmi $_v S₂ (ako to znazorńuje obrazok), pretoże każdy bod usecky S₁S₂ leżi vo vnutri kruźnice k_x alebo vo vnutri kruźnice k₂. Bod M, ako bod spolocnej dotycnice, leżi zYonku oboch krużnic. Preto spłynie bod M s Yonkajśim stredom rovnol’ahlosti E oboch krużnic.

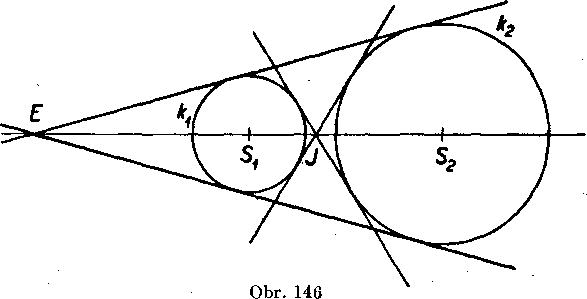
Z predchadzajueej uvahy vyp]yva tato konstrukcia spolocnych dotycnic: Zostrojime Yonkajśi stred rovnorah!osti E oboch krużnic (obr. 145). Bod E padnę zvonku kruźnice k_v Tomuto nasvedcuje obrazok, ale presYedcime sa o tom aj tak, ked’ vypocitame ve!kost usecky 8_±E. Z konstrukcie bodu E vyplyva vztah

ciże

Z toho dostaneme a dalej

SjE __ r_t S₂E - r₂ ’

S_XE r,

. -ĄE — SiS, ~~ r₂' r₂.8jE = r^SjE — r₁.S₁S₂

thetoże je

$1^2 U ' ^2>

je

SiE >    • (^ri — ^r*) = ^rv

^rl ^r2

Z bodu E móżeme teda viesf dve dotycnice t_v t₂ ku krużnic! k_x (obr.

v

145). Jtovnol’ahlost so stredom E a koeficientom ~ prevedie każdu

z dotycnic t_v ć₂ do dotycnice kruźnice fc₂, a tak sme spoloćne dotycnice zostrojili.Inespoloc-ne dotycnice nie su.

Poznamka. Ak maju kruźnice k_v k₂ imi vzajomnu po-lohu neź v priklade 10, pre spoloćne dotycnice nastanuine moźnosti. Napr. na obr. 146 su dve kruźnice, które leżia mimo seba; tu ] eźia obidra stredy rov-nolahlosti zvonku oboch krużnic; ku kruźniciam możno vicsf 4 spoloćne dotycnice (dve von-kajsim stredom a dve stredom vnutornym). Toto je najyacsi możny pocet spolocnych dotyc-    Obr. 147

nic dvoch krużnic.

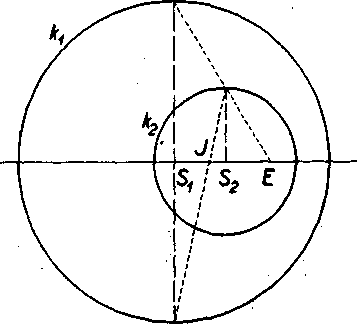
Na obr. 147 su dve kruźnice, z których jedna leżi vo vnutri druhej. Tu leżia oba stredy rovnol’ahlosti yo vnutri oboch krużnic; kruźnice nemaju spolocnu dotycnicu.

Niektóre pripady konstrukcie spolocnych dotycnic dvoch krużnic preberiete v cvićeniach.

Cvićenie

1.    Urćte mnożinu bodov, które rozdeluju tetivy, vychadzajuce z dane-ho bodu kruźnice v danom pomere A.

2.    Je dana krużnica k a bod A, który leżi yo vnutri kruźnice k. Urćte tetivu kruźnice k, ktoru bod A rozdeluje v pomere 4 : 1. Navod: Skumajte kruźnicu, do której prejde krużnica k rovnolahlosfou

so stredom ias koeficientom--