1954 Geometria 026

Ak je M taky bod a ak opiśeme krużnicu (M; r), dotyka sa tato kruż-nica priamky p a vytina na priamke q usecku dlżky d.

c) Diskasia. Vżdy zostrojime dve różne rovnobeżky p_v p₂. Rovno-

beżky q_x, q₂ możno zostrojit, ak je — sS r, ciże d 5S 2r. Źiadna

£

z priamok p_v p₂ nie je rovnobeżna so żiadnou z priamok q_lt q.₂. lebo p, q su róznobeżky. TJloha ma teda aspoń jedno riesenie, ak

d ^ 2r;

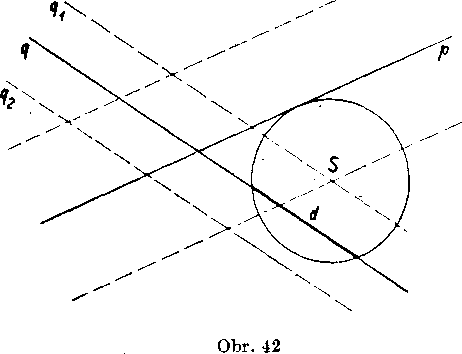
to je podmienka riesiternosti. Każdy z priesecikov p_v q_x; p₂, ą_x\ p_vq₂; p₂, q₂ dava jedno riesenie. Je vżdy p_x ^ p₂; ale może byt q_x = q₂, a to len v pripade, ked d = 2r.

tiloha ma teda 4 rieśenia, ak d < 2r, 2 rieśenia, ak d = 2r.

Pri rieseni konśtrukcnych uloh poużivame ćasto mnożiny bodov, vyhovujuce urcitej podmienke; byva to spravidla jedna priamka alebo niekolko priamok, ćasf priamky, krużnice a pod. V predoślom priklade boli tieto mnożiny (mnożiny stredov krużnic) dvojice rovnobeżiek. Oboznamime sa este s jednou takouto mnożinou bodoy, która je v uzkej suvislosti s obvodovym uhlom.

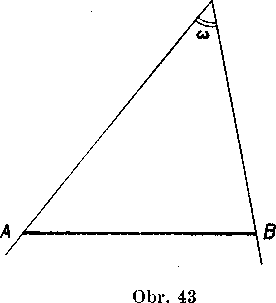
Vyrok: „TJsećku AB vidiet z bodu X pod uhlom of, znamenato, co znazorńuje obr. 43. X je bod leżiaci mimo priamky AB a <£ AXB = to.

Plati veta:

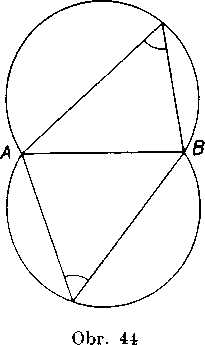
(9) Mnożinu bodov X, z której vidief usecku AB pod danym uhlom co, troria vsetky body dvoch oblukoy krużnic sumerne zdrużen^ch podia priamky AB s yynimkou bodov A, B (obr. 44).

Dokaż. Nech je jeden bod nasej mnożiny (obr. 45). Zostrojime krużnicu k opisanu trojuholniku ABX₁ a vo ynutri polroviny ABX₁ zvolime bod X na krużnici k. Podia vety (8) je potom <£ AXB — = AX₁B = <x>. Każdy bod X obluka AX₁B patri teda nasej mnożine bodov.

Vo vnutri polroviny ABX_x zvol’me bod Y mimo krużnice k. Zo-strojme krużnicu k' opisanu trojuholniku ABY. Stredy S, S' krużnic k, k' leżia na osi usecky AB a su zrejme różne (obr. 45); preto su różne aj uhly <£ ASB, <£ AS'B. Z toho vyplyva podia vety (8), że <C AXB ^

<:E A YB. Bod Y nepatri teda nasej mnożine bodov.

Tu istu uvahu, ktoru sme robili pre polrovinu ABX_V móżeme robit aj pre poirovinu opacnu. Naśa mnożina bodov sa teda składa z dvoch oblukoy sumerne zdrużenych podia priamky AB, co sme mali dokazał.

Poznamky. 1. Body A, B nepatria k hladanej mnożine bodov.

2.    Ak je uhol co pravy, su obidva obluky zhodne polkrużnice. Hlada-na mnożina bodov je teda krużnica, zostrojena nad priemerom AB ^s Yylueenim bodoy A, B.

3.    Na zostrojenie stredov krużnic, których ćastami su obidva oblu-ky, poużiyame pri kosom uhle co tento postup (obr. 46):

27