1954 Geometria 292

2. Ak namiesto jedineho polomeru o zyolime postupnosf (2) polo-merov

Pi > &2> 93 > ■ ■ ■ > P» > • • •

tak, aby

_ 1

P» — 2 Sn-V

a ak pre każdy clen tej to postupnosti urobi me uvahu podia odseku 1 dókazu tejto vety, dostaneme postupnost (5), której n-ty clen je ;

d.

otrą

71

+ TT 9 n

180 ' 2

Limit tejto postupnosti jestyuje a rovna sa

lim d,

0_n

= lim »->co

(Ttrcc _] 7t ^

180 ⁺ ~2 ^eV

= lim oo

nra

180~

71

+ 7T^lim Sn

nr ot 180

u-^-oo n~+oo \ 180 eim sme vetu 4 dokazali.

Poznamka. Zo vzorca pre dlżku obluka krużnice, której polomer je d!żkova jednotka, t. j. zo vzorca

^J «~>oo

!TC

⁼ I8Ó

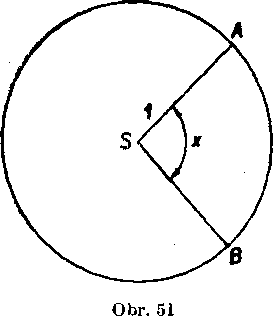
(dlżku obluka tento raz oznacujeme x) vyplyva, że dlżka obluka prislu-ehajuceho k stredovemu uhlu -ścASB, ktoreho vel’kosf sa v uhlovej miere royna <x, je priamo umerna ćislu a.

Dlżka

JT0C

Tso

tokto obluka sa zho-

duje s veIkosf,ou uh la <X A SB v oblu-kovej miere; oznacujeme ju arc <x (ći-tame arkus alfa) alebo iednodueho x. Teda

not

⁼ ISO ’

ix =

180x

71

Uvedene vzorce umożńuju premieńat oblukovu mieru na stupnovu a obratene. V praxi robime tuto premenu pomocou tabuliek.

Ak je dany vysek kruhu o polomere r patriaci k stredovemu uhlu <?; A SB, ktoreho yelkosf v oblukovej miere je x (obr. 51), potom obsali tohto vyseku

1

2

xr^l.

P =

Dlżka obluka krużnice prisluchajuceho k uhlu <$! A8B je

d = xr.

Cvicenie

1 j V ods. II. (str. 286) sa hovori, że utvar na obr. 43 sa składa z bodov YŚetkycłi kruhov o polomere o, które maju stredy na usecke AB. Dokażte, że sa tento obrazec składa z bodov krużnic o polomere q so stredmi na usecke AB.

2.    Postupom opisanym v odseku II. tejto kapitoly dokażte, że

a)    obvod roYnobeżnlka so stranami a, b rovna sa

d — 2(a + 6);

b)    obvod trojuholnlka so stranami a, b, c rovna sa

d == d ~k b “k c.

Navod. Pozri obr. 82 a, b.

3.    a) Obsah kruhu je P; urcte dlżku prislusnęj krużnice. . b) Dlżka krużnice je d; urcte obsałi prisluśneho kruhu.

4'; Ako sa zmeni obsah kruhu, ak dlżka prisluśnej krużnice vzrastie a) n-krat,

$) o s.

r?i Dany je sucet m dlżok dvoch krużnic a pomer p ich polomerov. IJrćte polomery tychto krużnic. VoIte m = 30, p — 3.

Jjf. VeIkosf daneho uhla v stupńovej miere vyjadrite v oblukovej miere

a)    180°, 90°, 270°, 45°, 135°, 60°, 30°, 225°, 330° (priamym vypoctom),

b)    26°35', 149°50', 312°45' (poużitim tabuliek alebo priamym vy-po£tom).

J. Vel’kost uhla daneho v oblukovej miere vyjadrite y stupnovej miere.

a) 2n,    -^-n, —% (priamym vypoctom);

Z Z o u 0

b)    0,75; 1; 2,35; *3 (poużitim tabuliek alebo priamym yypoótom).

$. Y krużnici o polomere 5 cm su dane dve tetivy AB = 7 cm, BC = = 8 cm. Urcte Yelkost tetiyy AC a prisluśneho stredoveho uhla.

293