1954 Geometria 164

Riesenie. V rovine a zvolime IubovoIny bod A: bod A zrejme neleżi v rovine g a uren je s rovinou g polpriestor qA. Ak je X A dalsi bod roviny g, leżi podia axiómy II priamka AX, a teda aj usecka AX v rovine a. Preto usecka AX neobsahuje nijaky bod roviny g, t. j. każdy bod roviny a prislucha polpriestoru g A.

Polpriamky a polroviny sme poużiyali v planimetrii na vytvorenie novych geometrickych utvarov. Tak napr. vieme, że usecka AB je mnożina yśetkych bodov spolocnych polpriamkam AB a BA; duty uhol ^.XYZ je mnożina yśetkych bodov spolocnych polrovinam

Obr. 22

YXZ a YZX. Podobnym sposobom poużijeme polpriestor a zavedieme novy pojem.

Definicia. Nech só dane dve rovnobeżne a na-yzajom różne roviny g, 0. Oznacme go ten polpriestor oddeleny rovinou g, który obsahuje rovinu a (pozri priklad 10), a go ten polpriestor oddeleny rovinou 0, który obsahuje rovinu g. Potom mnożi-nu bodoy spolocnych pol-priestorom g0 a 0g nazye-me vrstvou go alebo ag. Roviny g a o budeme na-zyvaf h ranionymi rovina-mi vrstvy.

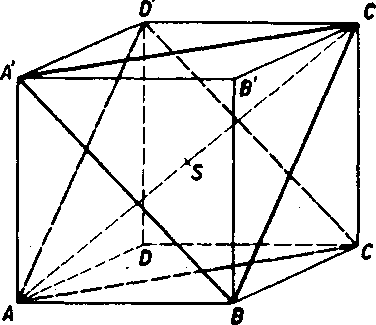
Priklad 11 (obr. 22). Je dana kocka ABCDA'B'C'D'. Marne do-kazat, że royiny A'0'B, ACD' urcuju yrstvu a że stred usecky AG' patri tejto yrstye.

Riesenie. a) Najskór dokażeme, że plati A'B |] CD'. Skutocne je AD \\A'D'd> AD || BO; pretoże roynobeżnost priamok je yztah tran-zitiyny, je A'D' || BC. Priamky A'D', BC leżia teda v tej istej rovine A'BC". Roviny ABB', CDG' su rovnobeżne podia kriteria rovnobeż-nosti rovin (veta 8). Podia vety 3 su roviny A'BC, ABB', CDG' vo yzajomnej polohe 2, t. j. priesecnice roviny A'BC s rovinami ABB', CDG' ćiże priamky A'B, CD', su navzajom rovnobeżne, ako sme mali dokazaf.

b) Obdobne ako v ods. a) by sme dokazali, że plati AD' || BO'.

Podia kriteria a rovnobeżnosti rovln su teda roviny A'C B', ACD rovnobeżne a urcujii vrstvu. Pretoźe usecka AC' prislucha jednak pol-priestoru A'C'B’A, jednak polpriestoru ACDC', prislucha aj ich spo-locnej ćasti, t. j. nimi urćenej vrstve.

Uż prv sme v cviceniach zobrazovali teleso nazyyane śtvorsten. Pomocou pojmu polpriestor móżeme styorsten presne definovat a tato

0

definicia je iba rozsiremm znamej definicie trojuholnika, ktoru ste pre-berali v planimetrii:

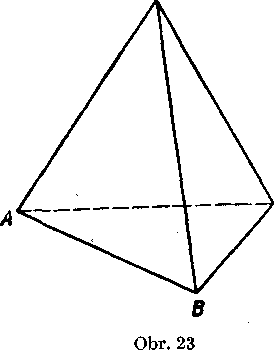
Dane su śtyri body A, B, C, D, które neleźia v jednej rovine. Tjtvar spolocny śtyrom polpriestorom ABC D; ABD C; ACD B; BCDA sa nazy-va §tvorsten (obr. 23).

VnutrajSkom stvorstena nazyva-me utvar spolocny vmitrajśkom sty-roch ypisanych polpriestoroy. Mno-żina bodov stvorstena, które nepatria k ynutrajśku stvorstena, tvori porrch Styorstena, Pomocou polpriestoroy móżeme definovat aj steny. Napri-klad stena ABC je utyar spolocny trom polpriestorom ABD C; ACDB; BCD A a rovine ABC.

TJsccky AB, AC, AD, BC, BD, CD nazyyame hrany stvorstena, body A, B, C, D yreholy Styorstena. Pomocou predoslych polpriestoroy alebo ich hranicnych bodov możno definovat aj tieto utvary.

Obdobu medzi trojuholnikom v planimetrii a stvorstenom v stere-ometrii możno pozorovat v mnohych ich ylastnostiach; s niektórymi prikladmi sa stretneme v dalśom yyklade.

Cvicenie

1. g je tenka nepriehladna rovinna stena, A bodovy zdrój svetla, le-żiaci mimo q. Predpokladame, że inak v priestore nie su nijake dalśie prekażky. Urcitu mnożinu bodov v priestore tvoria osvetlene body, inu body v tieni. Popiste a vysvetlite stereometricky.

2i Dokażte, że móżu existovat dva polpriestory qA a oB take, że ^: - każdy bod polpriestoru oB leżi v qA, ale nie naopak. Aku polohu maju roviny q a a a aku body A, BI

165