1954 Geometria 100

Pretoże uhol <f_BAC je tupy, je aj <f.BXC tupy; bod A’ nemóże teda spłynut s nijakym bodom X leżiacim medzi A, D. Dokazali sme teda, że

DA' > DA.

Podia znanie j vety zo 7. rocnika je

(2)    A'B>AB, A'0 >AC.

Podia PytagoroYej vety je v§ak

(3)    BC² = A'B² + A'C²; spojenim vztahov (2), (3) dostaneme vztah (1).

Pytagorovu vetu możno obratit takto:

Veta 3. Ak plati pre vel’kosti stran trojuholnika vzt’ah

a² = 6² + c²,

je trojuholnik pravouhly, a to tak, że pravy uhol leźi oproti strane a.

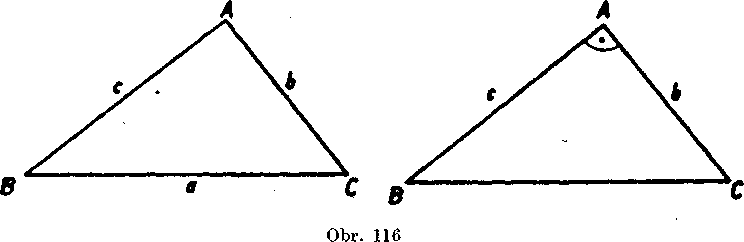
Dokaż. Dany trojuholnik oznacme ABC (obr. 116). Zostrojme pravouhly trojuholnik A'B'C' tak, aby bolo <)' A' — 90°, A'B' — c, A'C = b. Potom podia Pytagorovej vety je

B'C'² = b² + c².

Pretoże b² c² = a², je B'C'² = a², ciźe B'C' = a (B'C aj a su kladne cisla). Preto podia vety sss plati

A ABC X. AA’B'C

z toho vyplyva <£ A — <£ A' = 90°, co sme malidokazat.

Obratenie Pytagorovej vety je velmi cenne: dovoIuje nam vvpoc-tom zistit, że urcity trojuholnik je praVouhly. Spósob, zalożeny na

obrateni Pytagorovej vety, poużivali uż stare narody na vytycovanie praveho uhla v prirode.

Priklad 3. Mamę dve navzajom rożne prirodzene cisla u.v (u > v). Dokażme, źe cisla u² — v², 2uv, u² -j- v² su vel’kosti stran pravouhleho trojuhołnika.

Rieśenie. Zostrojime pravouhly trojuholnik, ktoreho odvesny maju yelkosti u² — v², 2 uv. Vel'kost jeho prepony yypoćitame podia Pytagorovej vetv

{u² — v²)² + (2 uvf = u‘¹ + 2u² v² + vⁱ = (u² + p²)².

Możno preto zostrojit trojuholnik, ktoreho strany maju yelkosti u²—v², 2 uv, u² v² a tento trojuholnik je pravouhly s preponou u² -j- v².

Poznamka. Pravouhle trojuholniky, które maju vel’kost stran yyjadrenu celymi cislami, volaju sa pytagorejske. Ńajznamejsi taky trojuholnik ma dlzky stran 3, 4, 5. Dostaneme ho, ak polożime v predchadzajucom priklade u =-- 2, v = 1. Ine zname pytagorejske trojuholniky maju diżky stran 5, 12, 13 (u ~ 3, v = 2), 15, 8, 17 (u = 4, v = 1), 7, 24, 25 (u = 4, v = 3), 8, 6, 10 (u = 3, v = 1) atd’.

Cvicenie

1. Pata vysky AP trojuholnika ABC leżi medzi bodmi B, C ą plati AP² = BP.CP. Dokażte, że <: BAC je pravy. Navod: Zostrojte prayouhly trojuholnik BCD s yrcholom D na polpriamke PA.

V akom yztahu je tato veta k vete Euklidovej ?

2.    Obdfźnik ma rozmery a, b; zistite podmienku pre to, aby pata kol-mice yedenej yrcholom na uhlo-priecku rozdelila tuto uhlopriecku v pomere 2:1.

Narysuj taky to obdfźnik.

3.    Trojuholnik ma strany a = 7 cm, 6 = 8 cm, c = 9 cm. Zostrojte śtvorec o rovnakom obsahu. Na-vod: Zostrojte najskór obdlżnik o rovnakom obsahu a potom po-użite postup z prikladu 1.

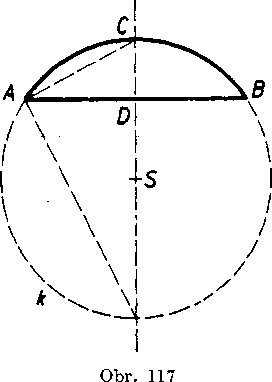
4.    Obr. 117. Kruhoyy odsekkrużnice k ~ (S; r) je obmedzeny tetivou

101