1954 Geometria 070

Priklad 2. Vyjadrite v atupńovej miere me dze pre uhol a, ktoreho yelkost pri jednotkovom pravom uhle je ]/3.

Rieśenie. Z tabuliek zistite, że

1,732 < y3'< 1,733.

Uhol ve!kosti 1,732 pri jednotkovom pravom uhle ma v stupńovej miere yelkost 1,732.90 = 155,88 ciże 155° 52' 48". Uhol ve!kosti 1,733 pri jednotkovom pravom uhle ma v stupnovej miere yelkost 1,733.90 = 155,97 ciże 155° 58' 12". Pre yelkost uhla a v stupńoyej miere teda plati

155° 52' 48" < a < 155° 58' 12".

Priklad 3. Marne rozhodnut, ci uhol fi yelkosti 0,7 pri jednotko-vom uhle 135° je ostry, prayy alebo tupy.

B

Obr. 83

Rieśenie. Ak je jednotkoyy uhol uhlom o verkosti 135°, ma prayy

2— -/ 21— ^ 20\ uhol yelkost — — 0,6. Pretoże 0,7 > 0,6 I 0,7 = —, 0,6 = -^-=— 1, o    '    \    oO    o 30/

je uhol fi tupy.

Cyicenie

1.    Ak vznikne uhol * grafickym odcitanim uhla fi od uhla y, je yelkost uhla « rozdielom yelkosti uhlov fi a y. Uokażtc to.

2.    Rozdelte euklidoysky dany uhol na 4 zhodne casti. Vypocitajte yelkost tychto casti, ked je yelkost daneho uhla 134°12'.

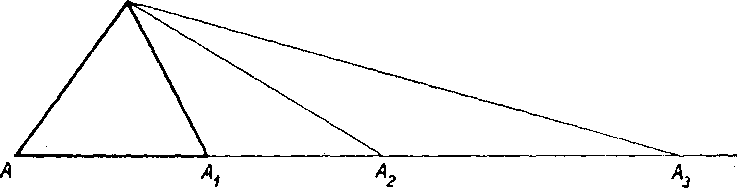
3.    Na obr. 83 je AA_XB rovnoramenny trojuholnik so zakladńou A_XB, A₁A₂B rovnoramenny trojuholnik so zakladńou A_tB, A₂A₃B royno-

ramenny trojuholnik śo zakladńou AJB atd'. Body A,A_l,A_z,A._i... leżia v priamke. Dokażte, że pre vel’kost uhIov plati vzfah

< AA & = ~^AA,B.

Viete tento vztah zovseobecnit ?

4.    Vypocitajte v stupńoch, v minutach a v sekundach vel’kost uhla, która je dana v stupńoch cislami:

11,63;    7^; 152,08.

5.    Ak je jednotkoyy uhol prayy, je yelkost uhla yyjadrena ziomkom

—, kde p. q su cisla nesudelitelne. Ake musia byt cisla p, q, aby

yelkost a) v stupńoch, b) v stupńoch a minutach bola yyjadrena celym ćislom?

6.    Styri body priamky su v poradi A, B, C, D. Bod F leżi mimo

priamky. Cisla x, y, 7. su po poriadku vel’kosti uhlov <r AVG, <$lBVD,    AVI). Yyjadrite yelkosti uhlov yt AVB, BVG,

«£ GVD.

7.    <x, fi, y su uhly trojuholnika. Dokażte, że uhly R +    — 4-/5 —

Z z ,

—-- y a A Y TT    y su dute. Vypocitajte ieh vel’kost,

Z    Z    Z    Z

4

ak je <% = — R, () = 82° (R znaci prayy uhol).

8.    Body C, D leżia vo vnutri tej istej polroyiny s hranicou AB, poł-priamka AB je osou uhla DAG. Dokażte, że pre yelkosti uhlov plati vztah

2 <£ BAE = BAG + <£ BAD.

2. Funkcia tangens

Zo 7. rocnika viete, że trojuholnik je urceny napr. dvoma stranami a uhlom, który je nimi zovrenf. To znaci, że ysetky trojuholniky, które narysujecie tak, aby mali za strany dane dve ńsecky a dany duty uhol za ynutorny uhol nimi zovreny, su zhodne. Na ktoromko[vek z tychto trojuholnikov móżeme potom zmeraf zvysnu stranu a zvyśne dva uhly.

71