1954 Geometria 248

Obsahy obrazcov ste yypocitali podl’a urcitych ylastnosti podobnych ylastnostiam 1. — 3. yelkosti usecky. Tymito vlastnos£ami sa vśak definuje aj obsah obrazca. Definujme si najpry obsah mnohouholnika takto:

Defini cia. Obsah mnohouholnika je cislo, które vyhovuje tymto podmienkam:

[1]    Obsah mnohouholnika je kladne cislo.

[2]    Zhodne mnohouholniky maju rovnake obsahy.

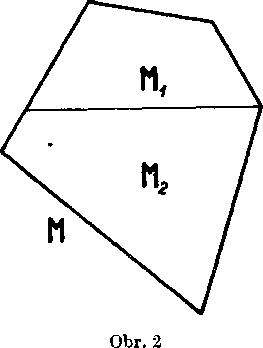
[3]    Ak sa mnohouholnik M składa z mnohouholnikov M_1; M₂, które sa navzajom neprekryvaju (obr. 2), rovna sa obsah mnohouholnika M suctu obsahov mnohouholnikov a M₂.

Obsah mnohouholnika jednożnacne urcime, ak doplnime podmienky [1], [2], [3] eśte touto pożiadavkou:

[4] Stvorec, ktoreho strana ma pri danej jednotkovej usecke vel’kost rovnu 1, ma obsah rovny 1 (tzv. jednotkovy stvorcc).

Ak priberieme eśte podmienku [4], móżeme dokazaf, że każdy mnohouholnik ma jediny obsah. To znamena, że każdemu mnoho-uholniku możno priradif jedine cislo tak, że su splnene podmienky

P]₇ą

Tuto dóleżitu vetu nebudeme dokazovat. ale overime si scasti jej platnosi na niektórych pripadoch. Ked’ odvodime napr. vzoree pre vy-pocet obsahu obdlżnika, dokażeme tym sucasne, że obsah obdlżnika je jednożnacne urceny podmienkami [1]—[4], Tym sme, prayda, eśte nedokazali, że obsahy obdlżnikoy, które sme vypoeitali podia odvodeneho vzorca, splnajunapr. podmienku [3].

Poznamky. 1. Ak su a, b, c kladne cisla a ak

je

c — a -\-b, c > a, c >b.

Preto vyplyva z podmienok [2], [3], że obsah mnohouholnika M je vacśi neż obsah ktorejkol’vek jeho casti M_x, M₂ (obr. 2). Na tuto po-znamku sa budeme v dalśom castejśie odvolavat.

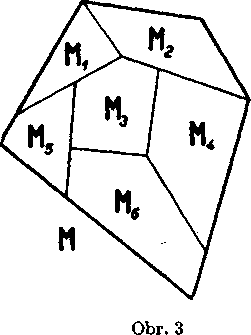
2. Podmienku [3], kde sa hovori o dvoch mnohouholnikoch M_v M₂, móżeme 1'ahko rozśirit na pripad, że mnohouholnik M składa sa z k mnohouholnikov M_1; M₂.M_k, które sa navzajom neprekryvaju (obr. 3, kde k = 7).

Teraz si strucne vysvetlime odvodzovanie niektórych vzorcov pre obsahy mnohouholnikov; naśou hlavnou ulohou pritom nebude ziskat vzorec, ale skór ukazat, ako sa opierame pri ich odvodzovani o podmienky [1]— [4] z definicie obsahu. Obsah mnohouholnika budeme dósledne oznacovaf pismenom P; ak budeme hovorit o stranach a, b, c, budeme tym mysliet na ich veIkost.

Veta 1. Obsah obdlżnika o stranach a, b rovna sa siiciim ab.

Vetu dokażeme postupne.

Obr. 4

1.    Ak a = b = 1, je dany obdlżnik jednotkovym śtvorcom, także podia podmienky [4] jeho obsah P sa rovna 1, t. j. v tomto pripade plati

P = a.b.

2.    Ak su a, b Iubovol'ne cele cisla, możno dany obdlżnik pokryt jed-notkoyymi śtvorcami v poetę a. b (obr. 4). Obsah każdeho z tychto śtvorcov sa podia podmienky [4] rovna 1. Obsah daneho obdlżnika sa potom podia poznamky 2 k definicii obsahu rovna

P = a.b.

3. Ak możno cisla a, b napisał v tvare

a = k.a', b = k.b\

249