1954 Geometria 020

Dalsi postup je ako v prvom pripade.

V tretom pripade je

AXB = /S —-a,    <£ AYB — y -j- d,

XA Y = 6 — x,    <£XBY=p + 7-

Dalsi postup je opat ako v prvom pripade.

2. Teraz dokaźeme: Ak je 8 stred krużnice a AYB obvodovy uhol prislusny k vacsiemu obluku, pripadne k polkrużnici, dava sucet uhla A8B (duteho alebo priameho) a 2<t AYB slyri prave uhly.

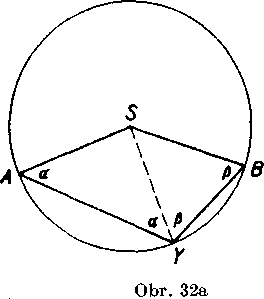
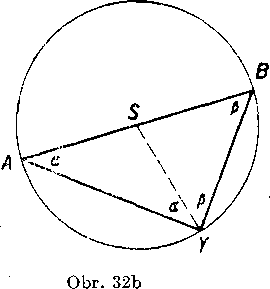
Dokaż: Obr. 32a,b znazorńuju dve możne polohy: bud’ stred kruż-nice, bod S, łeżi mimo tetivy AB, bud’ leżi na tetive AB. Na obidvoch obrazkoeh su rovnakymi cislicami oznaćene zhodne uhly v rovno-ramennych trojuholnikoch. Je teda

2<t AY8 + <£ ASY = 2R,

2<Y BYS + <£ BSY = 2B.

Scitanim obidvoch tychto vztahov dostaneme żiadany yysledok, lebo <£AYS + <BYS= AYB a <c ASY + BSY je uhol <£ ASB.

3. Teraz uż Tahko dokaźeme vetu (8). Ak je A YB obvodovy uhol prislusny k \ acsienni obluku AB, je prislusny stredovy uhol 4R — <£ A SB a to je podia ods. 2 uhol 2<£ A YB.

Ak je AYB obvodovy uhol, prislusny k polkruźnici, je prislusny stredovy uhol priamy, t. j. podia ods. 2 plati 2J.4 YB = 4R — 2R = = 2R. Obvodovy uhol <£ A YB je v tomto pripade pravy.

Ak je AXB obvodovy uhol, prislusny k mensiemu obluku AB,

a AYB obvodovy uhol, prislusny k zvyśujucemu yacśiemu obluku, je podia ods. 1

<£ AXB + <£ AYB = 2R

a podia ods. 2

3 ASB + 2 <£ AYB = 4R.

Z tychto dvoch vzt’ahov vyplyva jednak

A: ASB = 4.R — 2 <£ A7.B,

jednajł t. j.

2 <£ AXB = AR —2 AYB, ^ ASB =' 2 «£ AZ5,

co sme mali dokazat.

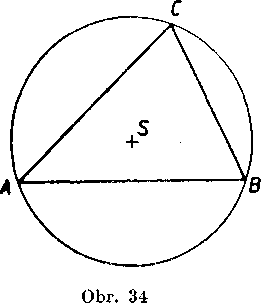
Poznamky. 1. Osobitny pripad vety (8), totiż tvrdenie, że każdy obvodovy uhol prislusny k polkrużnici je pravy, je znamy uż od staro-veku a nazyva sa yetou Taletovou.

2. Z vety (8) vyplyva, że obvodovy uhol prislusny k mensiemu obluku je ostry (jeho dvojnasobok je uhol duty) a obvodovy uhol prislusny k yacsiemu obluku je tupy (jeho dvojnasobok je uhol vypukly).

Na zaklade vety (8) o obvodovych uhloch urcujeme vel’mi ca^to uhly zoyrete różnymi tetivami krużnice. Uvedieme priklad.

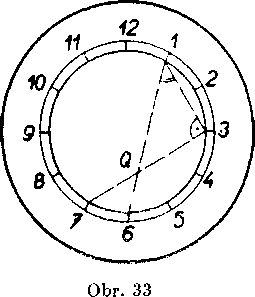
Priklad 1. Na ciferniku hodin spojime ,,body“ 1, 6 a 3, 7. Ake uhly zvieraju tieto priamky?

Rieśenie. (Obr. 33.) Oznacme Q ich priesecik. Potom <£ 613 je obvodovy uhol, prislusny k mensiemu obluku 36;. prislusny stredovy

21