1954 Geometria 044

Zakladnym pojmom v naukę o podobnosti je pomer dvoch useSiek; tymto pojmom rozumieme podiel ich yelkosti pri tej istej jednotkovej usecke.

Z predchadzajueej vety je zrejme, ze pri urcovani pomeru dvoch useciek nezależi na voIbe jednotkovej usecky. Oznaćme x_lt x₂veIkosti useciek A_XB_V A₂B₂ pri jednotkovej usecke e, k ve!kost useóky e pri jednotkovej usecke /, y_v y₂ veIkosti useciek AjĄ, A₂B₂ pri jednotkovej usecke /. Potom plati

«/i — kx i,    y₂ = kx₂,

a teda

₌₌ ®i

y₂ x₂

Priklad 6. tJsecku dlżky 5 cm mamę rozdelit na dve usecky v po-mere |^3 : 2.

Rieśenie. Vypocitame yelkosti obidvoch useciek. Ak yelkost prvej

oznacime * (cm), je vel'kos£ druhej 5 — x. Z danej podmienky vyplyva *1

x _]/3 5 — x ~ ~2~‘~

Koreń tej to rovnice je

*⁼2+P ^{= 5<2l/?_3)}-^2,32;

druha usećka ma vel’kosf

5 — x = 10 (2 — p”) == 2,68.

Z vypocitanych vel'kosti móżeme zostrojit usecky.

Priklad 7. Danii usecku AB marne rozdelit na dve usecky, których pomer budę dane cislo k < 1.

Rieśenie. Zvolime usecku AB ako jednotkovu a oznacime x veIkos£ prvej casti; potom je 1 — * ve!kos£ druhej casti. Z danej podmienky vyplyva

k,

ciźe

x (1 + k) = k.

Tato rovnost uyjadruje, że obdlżnik s rozmermi k, 1 ma ten isty obsah ako obdlżnik s rozmermi x, 1 + k. Z toho móżeme urcit usecku ve!kosti x konśtrukćne (obr. 62).

Zostrojime obdlżnik ABOD, ktoreho jedna strana je dana usecka AB a jeho druhy rozmer je BC = k (pri jednotkovej usecke AB). I)alej zostrojime (obr. 62) obdlżnik AEFD s rozmermi 1 + le; k. Zostrojime

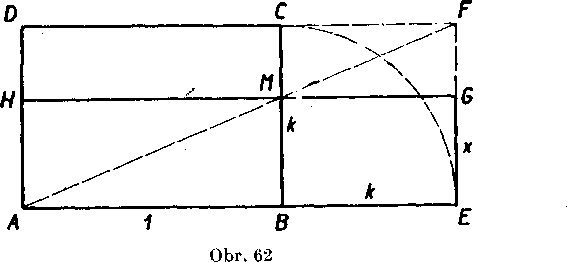
jeho uhlopriecku AF; priesecik priamok BC, AF oznacime M a vedie-me nim priamku Gil || AB. Zo zhodnosti vzniknutych trojuhołnikov vyplvvaju pre ich obsahy tieto yzfahy:

A ABM = A MHA, A MGF = A FGM, A AEF = A FDA.

Preto o obsahoch obd!żnikov plati:

BEGM = &AEF — A ABM — A MGF = A FDA — A^^ —

— A FCM = HMCD,

a dalej

A EG II = AB MII + BEGM = ABM 11 + HMCD = ABCD.

Obsah obdlżnika ABCD je vsak 1. k = k. Strana A E obdlżnika AEGH

ma ve!kosf 1 + k. Susedna strana EG ma teda vel’kost -——y == x.

1 łc

Tymto je zostrojena usecka ve!kosti x.

Priklad 8. Marne dokazaf, że pomer uhlopriecky a strany stvorca

jep : 1.

Rieśenie. Poużijeme ten isty postup ako v priklade na str. 35. Ak

45