1954 Geometria 246

14.    Pozorovatel’ letec, który je vo vyske v nad povrehom zemegule (S; r), vidi urcitu cast povrchu, ohranićenu vedIajsou krużnicou o polomere q. Urćte vzfah medzi velieinami v, r, q.

15.    Aky je polomer rovnobeżky v zemepisnej slrke <p {(p — 49°10')?

Aka je vyśka guToveho pasa medzi obratnikom raka a sev. polarnym kruhom {(p₁ — 23°30',    = 86°30')? Ako polomer zeme

gule berte r — 6 380 km.

16.    Znova uvaźujte o vzajomnych polohach dvoeb gu!ovych plócb a zistite, v ktorom pripade existuju spolocne dotycnice obidvoch plócłi a ćo tvoria.

11. POSTUPNf ROCNIK

I. OBSAHY MNOHOUHOLNIKOY

1. Obsah mnohouholnika

V    9. rocniku sme zavicdli dva dóleżite pójmy: veIkosf (dlżku) usecky a vel’kost uhla. Vel'kosf usecky sme definovali tymito vlastnos£ami:

1.    VeIkost usecky je kladne cislo.

2.    Zhodne usecky maju rovnaku vel’kos£.

3.    VeIkosi suctu dvocli useciek rovna sa suctu ich veIkosti.

Okrem toho urcita pevne zvolena usecka ma veikos£ rovnu i (je to tzv. jednotkova usecka). Tymito vlastnostami je uplne urćeny pojem veIkosti usecky. Podobne sme zaviedli vel’kos6 uhla.

V    6. a 9. rocniku sme vśak urćovali aj obsahy rozlicnych obrazcov (trojuholnika, rovnobeżnika, kruhu a pod.). Możno teda aj obrazcom priradit veIkosf, ktoru nazycame obsah obrazca.

VeIkos£ obrazca je vśak zlożitejśi pojem neż veikosfi usecky. Vieme, że każde dve zhodne usecky maju rovnaku veIkosf, a opacne, każde dve usecky o rovnakej yelkosti su zhodne. No pri vel’kostiach obrazeov su pomery uplne ine. Kod ste v 6. triede vypoćitali obsahy rozlicnych

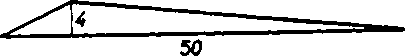
10

10

Obr. 1

obrazcov, videli ste, że dva obrazce móżu mat roynaky obsah, ale uplne odliśny tvar, t. j. nie su zhodne. Napr. stvorec o strane 10 ma obsah 10² = 100. Rovnaky obsah ma trojuholnik o strane 50 a vyśke 4 (obr. 1). Bezpochyby, nijakym pohybom nemożno tieto obrazce stotożnit, a preto nie su zhodne.

247