1954 Geometria 058

3.    Obr. 71. Bod D je patou vyśky trojuholnika redenej z vrcholu B, M je stredom strany AB, S stredom opisanej krużnice a < C je ostry.

a)    Dokaźte, że plati A ASM ~ A BGD.

ctc nhr

b)    Odvod’te z toho vzfah r = — = —, kde P je obsah trojuholnika, r polomer opisanej krużnice, v_b ve!kost vyśky.

4.    JKL je rovnoramenny trojuholnik so zakladńou JK, <£ J = 72°, M je taky bod usecky KL, że polpriamka JM je osou uhla J.

a)    Dokaźte, że plati A JKL ~ A KMJ.

b)    Odvodte z toho vzt’ah LM = ]/KL .KM.

Navod: Uvażte, że A JLM je rovnoramenny.

Obr. 72

5.    Napiśte vzorec pre vysku a obsah rovnostranneho trojuholnika, ktoreho strana ma dlżku a. Vypocitajte pre a — 8,6 (cm).

6.    Obdlżnik s rozmermi 5 cm, 8 cm ma ten isty obsah ako obdlżnik, ktoreho jeden rozmer je y50. Vypocitajte druhy rozmer a zostrojte ho s poużitim prikladu 6.

7.    Obr. 72. Tień stromu ma dlżku 35 m, tień kol mej metrovej tyce ma v tom istom case dlżku 148 cm. Vypocitajte vyśku stromu. (Slnećne luce povażujeme za rovnobeżne.)

8.    Dane su róznobeżky VAB a VG. Krużnica opisana trojuholniku ABC pretne priamku VG este v bodę D. Urćte vzdialenosf VD\ poużite priklad 7. Może sa stat, że je VG -=■ VD?

9. Ak plati v trojuholniku 2? = 2 <£ C, je b² = c (r -f- «). Dokaźte to. Navod: Na predlżeni usecky AB za bod B zostrojte bod D tak, aby bolo BD — CD a dokaźte, źe A -ABC ~ A ACD.

10. Bod A leź! vo vnutri krużnice A: — (S; r). Dve secny nim vedene pretnu krużnicu k vo dvojiciach bodov K, L; M, N. Dokaźte (podobne ako v prlklade 7), że plati

AK.AL = AM.AN.

3. Balsie vety o podobnosti ti'ojuholnlkov

Yetu 2 możno obratif, a to tak, że z podobnosti dvoch trojuholnikov vyplyva zhodnosf każdej dvojice uhlov k sebe prislusnych. Prebladno vyslovene:

Veta 3. Ak je A ABC ~ A A'B’C', je <£ A = <£ A', B = ^ B' a C = <(C C'.

ć    c

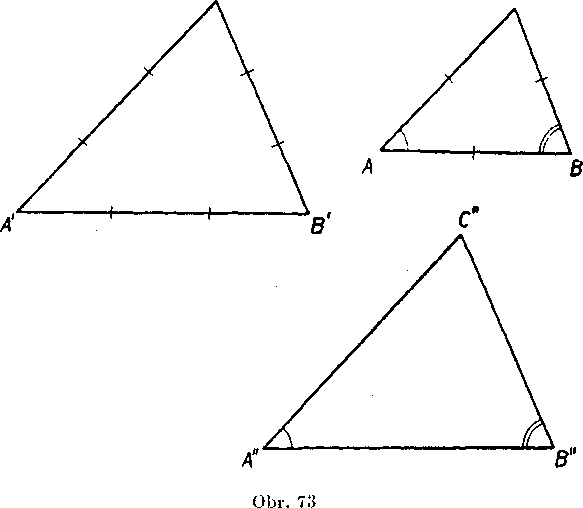
59