1954 Geometria 182

aspoń jedna strana je rovnobeżna s n. Kosouhly rovnobeżnik vsak tież może mat za pravouhly priemet do rc obdlżnik a aj priemetom obdlżni-ka może byt kosouhly rovnobeżnlk. Obidva tieto pripady si vysvetlite v cvićeni.

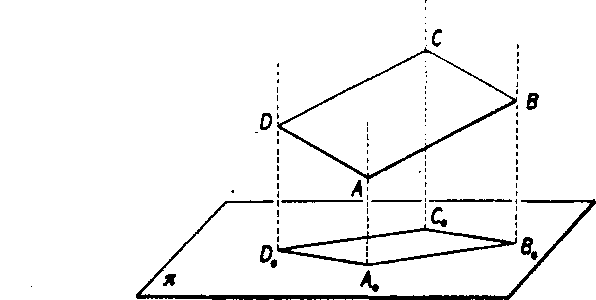
Obr. 37

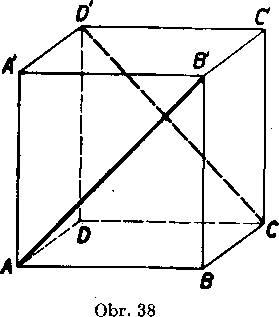
Treba sa zmienit eśte o tom, ako sa dve kolmice a dve kolme roviny znazornuju vo vo!nom rovnobeżnom premietani. Kolmice sa zobra-zuju ako kolmice len vtedy, ak je rovina, która je rovnobeżna s oboma priamkami, rovnobeżna aj s nakresńou (napr. priamky AB' a CD’ na kocke, obr. 38). Inac si musime pomahat tym, że kreslime niektóre skreslene utvary v ich skutoćnom tvare v pomocnych rovinach a potom

sa snażime v nich urobifi konśtruk-cie.

Priklad 4. Je dana kocka ABCD A'B'C'D' (obr. 39a) v zakladnej po-lohe a body K, L, H, które leżia postupne vo vnutri hran A'B', A'D', AA'. Z bodu A' ved’te kolmicu na rovinu KLH a urcte patu P; zobrazte vo vol’nej projekcii.

Riesenie. Kolmicu A'P najde-me ako priesecnicu dvoch rózno-beżnych rovin, sućasne kolmych na rovinu KLH (veta 20). Za jedhu z tychto rovin zvolime rovinu a, która prechadza bodom A' a je kolma na priamku HK (a tym na rovinu KLH). Prieseeik L' s a.HK najdeme ihned, lebo obidve kolmice A'L' a HK sa zobrazuj u ako kolmice. Rovina a dalej prechadza bodom L, lebo A'L je kolme na HK. Je teda rovina a dana bodmi A', L, L' a jej priesecnica s rovinou KLH je priamka LL'.

Za druhu rovinu r zvolime rovinu vedenu bodom A' a kolmu na priamku KL. Ako v predchadzajucom pripade zistime, że rovina r ide bodom H a bodom II', kde H' je patou kolmice vedenej bodom A' na KL. Ale obraz kolmice A 'H' nie je teraz koimy na obraz priamky

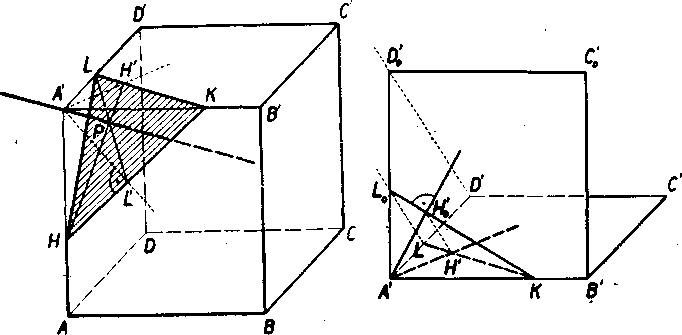
Obr. 39a    Obr. 39b

KL. Preto zostrojime v pomocnom obrazku 39b stenu A'B'G'D' v sku-tocnej ve!kosti a v skutoćnom tvare, cim dostaneme stvorec A'B'CqDq. Bod K móżeme priamo preniesf na hranu A'B', bod L₀ (obraz bodu L) zostrojime podia dohovoru (d) na str. 147, że rov-nobeżne usecky sa skracuju v rovnakom pomere. Pri konśtrukcii po-użijeme teda rovnoIahle trojuholniky A'D'D'₀ a A'LL₀. Teraz je aj obraz A'-H'₀ kolmice A'H' koimy na obraz priamky KL, t. j. na priamku KL₀. Takto dostaneme obraz H'₀ paty kolmice a znovu pomoeou rovnol’ahlych trojuholnikov KLL₀ a KH'Hó najdeme obraz H' paty kolmice, który prenesieme spat do obrazu kocky. Bodmi A', H, H' je urcena rovina t a jej priesecnica s rovinou KLH je HH'. Teraz uż marne bod P = LL' .HH’, a tym aj hladanu kolmicu A'P.

Priklad 5. Je dany śestboky hranol, obmedzeny dvoma zhodnymi pravidelnymi śestuholnikmi ABCDEF a A'B'C'D’E'F’ a śiestimi

183