1954 Geometria 052

vcta 1. Ak je A A_XB_XC_X ~ A A₂B₂O_z a A A₂B_tC₂ ~ A A₃B₃C₃, je aj A A_XB_XC_X ~ A A₃B₃C₃.

Dókaz: Podia predpokladu możno najst kladne cisla k, m tak, że plati:

A_zB₂ = k .A_XB_X, B₂C₂ = k . B₂C₁. C₂A₂ = k .C_XA_X;

A₃B₃ ~ ^•■^/^gB₂, ^Sp₃ ⁼ in.Byp₂, O.jAg =

Ak dosadime z prvych troch vztahov za A₂B₂, B₂C₂, C₂A₂ do druhych troch vztahov, dostaneme

A₃B₃ — km.A_xB_x, B₃C₃ = km,.B_XC_X, C₃A₃ = km.G_XA_X, kde km je kladne cislo; trojuholniky A_XB_XC_X a A₃B₃C₃ su teda podobne.

Podobnost dvoeh trojuholnikov nezistujeme spravidla podia ich stran, ale podia ich uhlov. Je to możne podia poueky, ktoru teraz odvodime.

Veta 2. Ak platia pre uhly trojuholnlkoy ABC, A'B'C' yzfałiy < A = < A', A 5 = A 5', potom je A ABC A A A'B'C'.

Strucnejśie, no menej urcite vyslovujeme vetu 2 takto: Ak maju dva trojuholniky dve dvojice zhodnych ynutornych uhlov, su podobne.

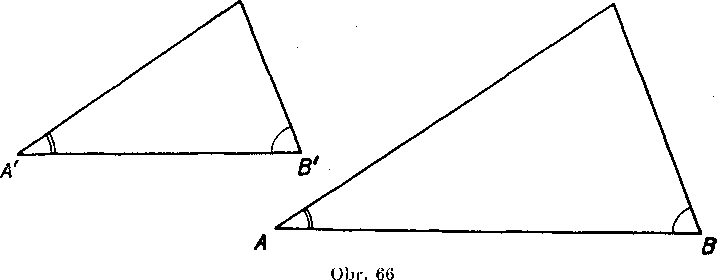
Dókaz (obr. 66): Dane su dva trojuholniky ABC, A'B'C'; pred-pokladajme, że su splnene predpoklady vety 2, t. j. że plati

<£ A = <£ A',    ^    B'.

Pomer useciek A'B', AB oznaćme k: je teda

A'B’ — k.AB.

Ak je k = 1, su obidva trojuholniky zhodne podia vety um. a teda aj podobne.

Ak je k ^ 1, uprayime oznaeenie obidvoeh trojuholnikov tak, aby platilo A'B' < AB (keby bolo A'B' > AB, vymenili by sme oznaeenie obidvoch trojuholnikov). Potom vśak plati vzfah k < 1.

C

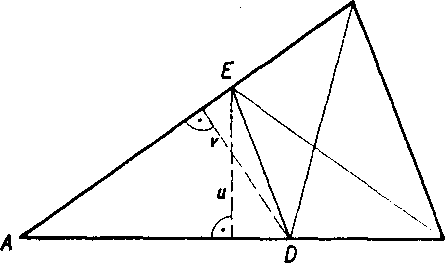
Obr. 67

Teraz premiestime trojuholnik A'B'C' tak, ako to znazornuje obr. 67, t. j. tak, aby bod A' preśiel do bodu A a body B', C' po poriadku na polpriamky AB, AC. To znamena: Na polpriamke AB zostrojime bod D tak, aby bolo AD = A 'B', a na polpriamke AC zostrojime bod E tak, aby bolo AE = A'C. Podia vety sux je A A'B'C' A A ADE. Ak dokażeme, że AE = k.AC, budę aj A'C' = k.AC. Obdobne dosta-neme, że B'C' = k.BC (tu treba premiestif, trojuholnik A'B'C' tak, aby bod B' presiel do bodu B a body AC po poriadku na polpriamky BA, BG). Tymto budę podobnosf obidvoch trojuholnikov dokazana.

Yratme sa teda k dókazu vztahu AE = k.AC. Na obr. 67 su zostro-jene dve vyśky trojuholnika ADE\ ich vel’kosti su oznacene u, v. Obsah trojuholnika ADE yyjadrime dvojakym sposobom; dostaneme

]-AD.u = ~AE.v

mt    £

53