1954 Geometria 324

c)    Urcte V — V, ak V znamena objem Zrezaneho kużela a V objem valca. Ćo z toho vyplyva pre pripad, ked’ sa vel’kosti r_x a r₂ mało lisia od seba? Vysvetlite vyznam rozdielu V — V'.

d)    Nech obvod stredneho rezu je o; upravte vzorec pre V' tak. aby v nom vystupovalo o (v lesnickej praxi sa hodnota o na-zyva paskova miera kmeńa).

35,    Komin tvaru duteho rotacneho zrezaneho kuźela ma vyśku 28 m. Urcte vahu muriva, ak spodne priemery su 3,7 m a 2,2 m a horne priemery l,8mal,2m(lm³ tehloveho muriva vażi 1,81).

36.    Kmeń stromu 18,5 m dlheho ma spodny priemer 0,65 m a vrchny priemer 0,35 m.

Urcte jeho objem, ak ho povazujete za zrezany rotaóny kużel; urcte jeho pribliżny objem podia sposobu v ulohe 34 b.

Obr. 75    Obr. 76

37. Streeha veże składa sa z dvoch ćasti; spodna casf ma tvar zrezaneho rotacneho kużela o priemere podstav 3,5mal,8ma vyśku 1,3 m, vrchna ma tvar rotacneho kużela s podstavou, która je totożna s mensou podstavou spodneho kużela a vyska je 3,5 m. Urcte objem priestoru pod strechou.

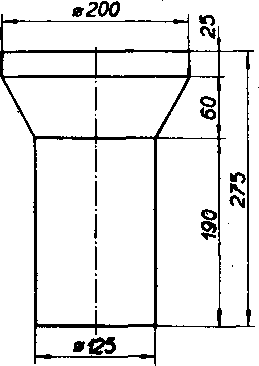
3.Ł Kolko litrov ma kanya zobrazena na obr. 75? (Vśetky dlżky su v centimetroch.) Aky objem (v m³) ma zasobnik na obr. 76? (Yśetky dlżky su v centimetroch.)

6. Objem gule a jej iśasti

Najpry vyslovime vetu pre objem gule a potom postupne urcime objem gul’oveho odseku, guIovej vrstvy a guIoveho yyseku.

4

Veta 7. Objem gule o polomere r rovna sa y nr³.

Dokaż. Na danej guli o strede S a o polomere r zvo!me si Iubovol’ny usek, ktoreho vyśka, oznacime ju v, royna sa nanajyys polomeru gule, teda v r.

Polomer podstavy zvo-leneho odseku nech je q.

Stredom gule polożime priemer gule, koimy na rovinu «, która z gule od-deluje zvoleny odsek (obr 77 zobrazuje rez gule rovi-nou prechadzajucou zo-strojenym priemerom).

Priesecik tohto priemeru s rovinou a oznacme P, priesecik priemeru s vrchlikom, który obmedzuje zvoleny odsek, oznacme Q; je teda PQ = v.

Deliacimibodmi P₀ = P, P_l,...,P_n = Q rozdelime vyśkuPQ useku

V

nanrovnakych casti (n > 1) veVkosti — (naobr. 71 zvolili sme n = 4);

roviny prechadzajufce tymito bodmi roynobeźne s ro vinou * pretinaju uvażovany usek v kruhoch (yynimku tvori rovina prechadzajuca bodom Q) obmedsenych krużnicami o stredoch v bodoch P₀, P_vP_n-_V Ich polomery oznacime postupne q₀ — o, n_v..., o_n _₁.

Podia Euklidovej vety yypocitamc z pravouhlych trojuholnikoy RQA₀, RQA,^..., RQA_n~_l (kde R je druby priesecik priemeru PQ₀ s gul’ovou płowkou a A₀, A_v A_n-_X su prieseciky priemeroy jednotli-vych zostrojenych krużnic s gu!ovou płochou) ich vyśky q² = v(2 r — v),

9)    9)    tfl _ I    _ 1

e! = (»-l)-(2r-* + y) = —«(2r-_W)+-^-«* =

n-

n

-e² +

(w —1)1

v,

(1)

325