1954 Geometria 260

Dokaż. Ak su mnohouholniky M, M' podobne, możno jeden z nich premiestit’ do takej polohy, że existuje royuolah łosi o strede S a pornere k(k ^ 1; k ^ 0), który ho prevadza do druheho mnohouholnika (obr. 2

16, kde k — —). Ak możno mnohouholnik M rozlożii na trojuholniky

O

Ai, Ag, •••, A»> potom mnohouholnik M' podobny mnohuholniku M możno rozlożifi na trojuholniky Ań Ań •••> Ań podobne v porad! trojuholnlkom, które vznikli rozkładom mnohouholnika M.

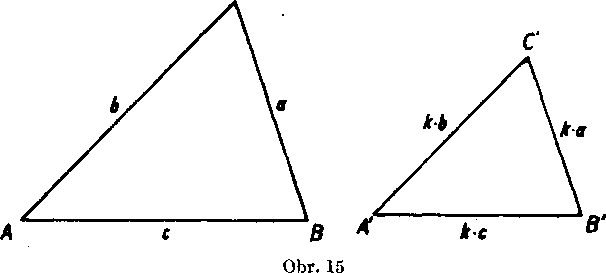
Mnohouholnik M rozlożime na trojuholniky    Ag, •••, An

(na obr. 16 n = 3) a ich obsahy oznacime P_t, P_a, ..., P_n. Pre obsah P mnohouholnika M plati (podia podmienky [3])

P = P_{1 +} P₂₊ ...-)- P_n.

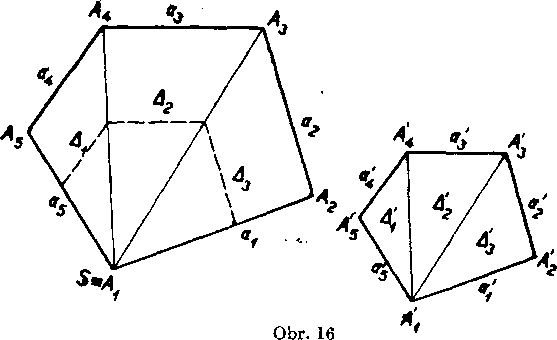
Mnohouholnik M' możno rozlożii’ na trojuholniky Ań Ań Ań podobne po poriadku trojuholnikom Ai, A2>    A»- Obsahy

trojuholnikov Ai, Ań • ••> Ań rovnajusa (ako vyplyva z predosleho) po poriadku IAP_V, k‘ⁱP₂, k²P_n. Pre obsah P' mnohouholnika M' plati

P' = k²P₁ + *^aP₂ + ... + k*P_n,

C1ZG

P' = k*(P₁+P₂ + ... +Pn).

Pretoże sa vyraz v zatvorke rovna P, je

P' = k*P.

Poznamka. Je zrejme, że pomer podobnosti dvoch «,-uholnikov MM sa rovna pomeru vel’kosti sehe zodpovedajucich stran (obr. 16), t. j.

= = = — a_x Cig

Pomer obsahov P', P obidvoch mnohouholnikoy

eiże

P;

P

= k\

p;

p

a{² aś²    ań²

a\~ a\    a\'

Posledny vz£ah yyjadruje, że obsahy podobnych «,-uholnikov (n A A 3) su v rovnakom pomere, ako druhe mocniny ve!kosti sehe zodpo-yedajucich stran.

IJloha. Je dany trojuholnik A ABC. Zostrojte priamky rovnobeżne so stranou AB tak, aby dany trojuholnik rozdelili na n casti o rovna-kom obsahu (obr. 17a, kde sme ułohu riesili pre n = 4).

Riesenie. Nech    M₂N₂, ...,    (obr. 17a) su hladane

priamky. Oznacme obsah daneho trojuholnika A ABC pismenom P a obsahy vzniknutych trojuholnikov

~ A^ńdf₂iV2    ~ ... ~    M_n^₁N_n-₁.

które su vśetky podobne trojuholniku A ABC po poriadku P_1; P₂, P₃, ..., Pn-j. Plati

Pi =

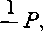
n

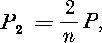
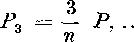
P_n-₁

n — 1 n

P.

261