1954 Geometria 224

dobnosti Je roynolahlost. Ak vieme teda napr., że utvary U, U' z pred-chadzajucej definicie su rovno!ahle, su utvary U, U_x podobne. To poużijeme pri dokaże nasledujucej vety.

Veta 37. Dve nayzajom roynobeżne roviny q aa, które nie su vrcho-love ani roynobeżne s niektorou vrcholovou priamkou ihlanoyeho priestoru, pretinaju ihlanoyy priestor v podobnyeh mnohouholnikoch.

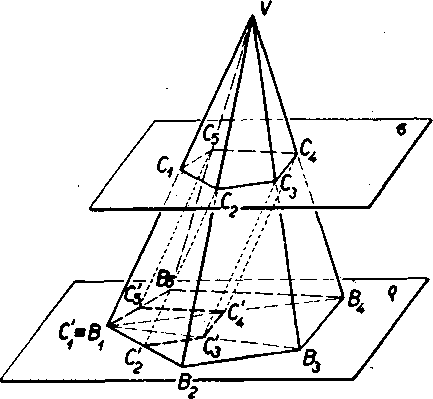
Obr. 81

a obdobne pre dalśie body. Całej je B₂B_S j| C'₂C_{ że n-uholniky B₂B₂.. ,B_n a C[C₂... G'_n

Dokaż (obr. 81). Priesekove mnohouhol-niky oznacme B₁B₂... B_n (v rovine q) a G_XG₂ ...(?„ (v rovine a). Zostrojme hranoloyy priestor s riadiacim mnobouholnikom G₁G₂ ... C_n a so smerom vrcholovych priamok p = VO_v Rovina o !|(T pretne tento hranol v ra-uholniku C[G₂.. ■ G_n, który je zhodny s C_lC₂.. ,G_n (yeta 35). Zrejme je C{ = B_v ĄĄ |[ C{C'₂', t. j. body B_v B₂, C₂ leżia na jednej priamke. Pre bod piat! B.B, || C&i, t. j. body B_vB₃,G_ależia na jednej priamke ₂wg ,atd’. Z toho vyplyva, v rovine q su rovnol’ahle so stredom rovnol’ahlosti v bodę B₁ = G{, a teda podobne, a preto aj mnohouholniky B₁B₂.. ,B_n a C₁C₂. . .C_n su podobne.

Teraz mamę ysetko pripravene k defimcii dalśich telies, tzv. ihlanoy.

Definicia. Oznacme I cast ihlanoyeho priestoru svreholom F,ktora je prilahla k riadiaeemu n-uholniku v rovine q, lltvar, spolocny utyaru I a polpriestoru qV, volame w-bokym ihlanom.

Riadiaci mnohouholnik je podstava ihlana, jeho strany su hranami podstayy, jeho yrcholy su vrcholmi podstayy ihlana. Yrchol F budeme teraz nazyvaf hlaynym yrcholom ihlana. Bocnymi hranami budeme nazyyat casti hran ihlanovej płochy, a to usećky ohranićene hlaynym yrcholom a yrcholmi podstayy. BoiSne steny su trojuholniky, leżiaee

v stenach prislusnej ihlanovej płochy. Podstava a bocne steny tvoria povrch ihlana. Body ihlana, które neprisluchaju k povrchu, tvoria ynutro ihlana a yolaju sa ynutornymi bodmi ihlana.

Trojboky ihlan volame casto osobitnym menom — §tvorsten. Który-kol’vek z jeho styroch vrcholov możno povażovat za vrchol hlavny' a ktorukol’vek z jeho styroch stien za podstavu.

Vzdialenos< hlayneho vrcholu od roviny podstayy vola sa vy8kou ihlana. Ak je podstayou pravidelny w-uholnik a ak je pata vysky stredom tohto pravidelneho n-uholnika, vo-lame ihlan pravidelnym łi-bokym ihlanom. Stvorsten sa vola pravidel-nym stvorstenom, ak su yśetky jeho steny zhodne rovnostranne trojuhol-niky. Możno ho teda atvorakym sposobom povażovat za pravidelny trojboky ihlan.

Priklad 3. B,ovina g , która je^₅ rovnobeżna s rovinou g podstayy \    / /Z

ihlana a która, pretina jeho boćnu \ j hranu vo ynutornom bodę, rozdęli ihlan na novy ihlan a na dalśie tele-so, które nazyyame ihlan zrezany.    _{0br g2}

Dokaż te :

a)    Obidve podstayy zrezaneho ihlana su podobne mnohouholniky.

b)    Yelkosti stran, które leżia v tej istej stene póvodneho ihlana, su v rovnakom pomere ako vyśky obidvoch ihlanoy (obr. 82).

Rieśenie. Ćast a) nasho prikladu bola dokazana vo vete 39. Odtial

A^A₂ _ A₂A₃ _    _ A_nA₁

/i\\ 'W ii \ \ k\ \
	w
A
ii \y, \
143	4ł

tież vyplyva, że _A stava teda dokazat, że k =

AfjAą

AM

v

v'

kde

v, v

—    ..... Pre ćast b) zo-

AM

su yyśky ihlanoy. Nech n

je vrcholovou rovinou AyZ, kde Z je patou kolmice, która je vedena yrcholom V na rovinu A₁A₂A₃. Ak oznacime Z' priesecik priamky YZ s druhou podstayou, ihned’ yidime, że trojuholniky A A[VZ^r, A A^VZ su rovnol'ahle so stredom roynolahlosti V. Z toho

yyplyya    = ~ =    balsie rovnol’ahle trojuholniky, a to

A VA₁A₂ a A VA[A₂, dostayame v rovine steny VA₁A₂. Z toho

225