1954 Geometria 290

obluka, nazveme postupnosf priradena danej usecke alebo obliiku

a vyslovime tuto zovseobecnenu definiciu dlźky:

Definieia. Dlźkou usecky, krużnice alebo jej obluka volame limit.

*»*

lim d

n~+CD

postupnosti (5) priradenej tej to "usecke, krużnici alebo jej obluku.

Poznamka. Ćleny postupnosti (2) polomeroY rznikli postupnym rozpolenim prveho ćlena, t. j. polomeru o_x. Możno vsak dokazat, że limit postupnosti (5) nezavisl od toho, akeho si zvolime prveho clena postupnosti (2). Dokonca namiesto postupnosti (2) bolo by możne zvolit akukol'vek nuloYu postupnosf s kladnymi clenmi. Postupnosf (2)

sme voliłi pre jej jednoduchosf.

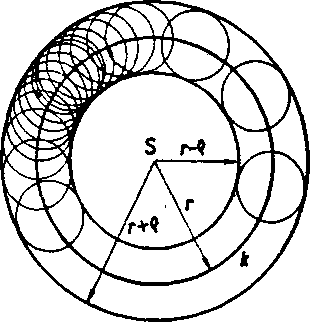
Obr. 49

Pomocou novej definicie dlżky odvodime vzorce pre vypocet dlżky krużnice a jej obluka.

Veta 3. Dlżka krużnice k o po-lomere r je

d = 2nr.

1. Nech je k dana krużnica o po-lomere r. Zvoł’me r > q > 0 a zestrój me krużnice so stredmi na krużnici k (obr. 49). Body tychto krużnic a ich vnutorne body vy-plnia medzikrużie, ktoreho obsah (ako sme ukazali v cvićeni 56) sa rovna

P_e = 4n g.r.

Ak tento obsah delime ćislom 2_e a ak podiel oznaćime d_t, potom

d_e= ~- = 2 nr. 2q

2. Ak namiesto jedneho polomeru ę zvolime postupnosf (2) polomeroY

6i > 02 > 63 >.....>{?»’••••

tak, aby

1

6n — 2 6»-l>

a ak pri każdom clene tej to postupnosti urobime uvahu podia odseku tohto dókazu, dostaneme postupnost (5), której łi-ty clen je

= 2n r.

^e« 2o_n

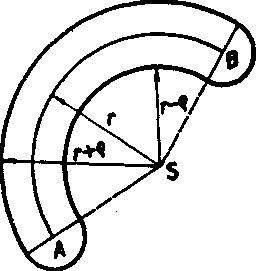
Obr. 50

Vśetky eleny postupnosti (5) royna ju sa v tomto pripade 2nr, takie limit tejto postupnosti je

lim d_c = 2n r, n-y oo ⁿ

eim sme vetu 3 dokazali.

Veta 4. Dizka obluka krużnice o polomere r prisMchajuceho k stredo-vemu uhlu <£ A8B (obr. 50)

nr

180

kde «je yelkosf uhla <c A SB v stup-novej miere.

1. Nech je AB dany obluk (obr. 50). ZvoTme r > g > 0 a zostrojme

krużnice o polomere g tak, aby ich stredy boli na obluku AB. Body tychto krużnic a ich vnutorne body vyplnia utvar na obr. 50. Tento utvar je podia blanku 2 (str. 270) obrazec, lebo ho możno zlożit z vy-seku medzikruzia o połomeroch r + q. r — g prisluchajuceho k stredo-yemu uhlu a a z dvoch polkruhov o polomere g. Obsah tohto obrazca je (podia cvi cenią 4 na str. 283)

bizę

n a '360

[(r + g)² — (r — p)²] + ng²,

360

(r² + 2gr + g² — r² + 2gr — g²) -j- rig²

n%

360

4 gr + tt?²;

P

.7 \ nr

90

+ ng²

Ak delime obsah P ćislom 2g a ak podiel oznacime d_s,

2g

nrtx

180

, ⁿ

+ Y^e-

291