1954 Geometria 284

Dana je krużnica k o polomere r. Zostrojte krużnicu k' o polomere r' >r tak, aby obsah kruhu obmedzeneho krużnicou k* rovnal sa obsahu medzikrużia urceneho kruźnioami k, k'. ZvoIte si r = 4 cm.

8. Zostrojte krnh, który ma rovnaky obsah ako dane medzikruźie.

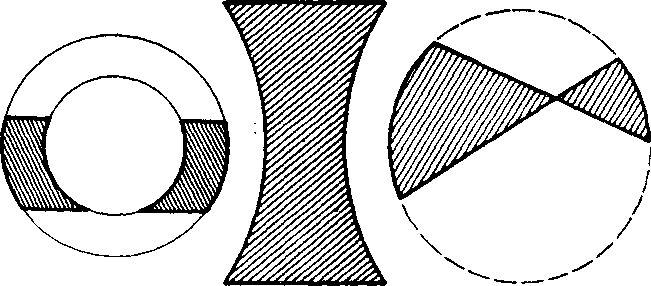
Obr. 38d    Obr. 38e    Obr. 38f

9. V krużnici o strede 8 je zostrojena tetiva AB. Zostrojte krużnicu k', której priemer je SA. Dokażte, że pre obsahy J\ a P₂ odsekor

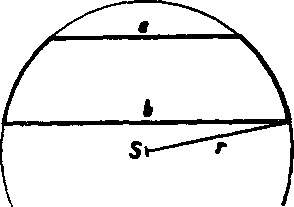
Obr. 39

prisluchajucich k tetive AB v da-nom a zostro jenom kruhu piat i

9. Dane medzikruźie rozdefte sii-strednou krużnicou na dve ćasti o rovnakych obsahoch.

10.    Ako sa zmeni obsah kruhu, ak je-ho polomer a) zvacśime, b) zmen-śime o e > 0 ?

11.    Urcte obsah medzikrużia vytvo-reneho kruźnioami o polomeroch r -{- g, r — q (0 < q < r).

2. Zoyseobecnenie pojmu dlżky. Diźka kiH-żłtiec

Y 9. rocniku sme v ućive o merani useciek zaviedli pojem vel’kosti ciże dlżky usećky ako ćisla, które mało vlastnosti podobne vlastnos-tiam [1] — [4] obsahu obrazca. V tejto ćasti budeme sa zaoberat dlż-kou krużnice a dlżkou jej obluka.

Prirodzene, najprv musime tieto pojtny definovat, pretoże pojem dlżky sme definovali iba pre usecku. Kym vyslovime prislusnu defini-ciu, zhruba naznaćime myślienkoyy postup, którym dójdeme k tejto definicii.

Keby sme mali v praxi urcit dlżku drótu, który ma tvar kruhoveho obluka, jednoducho by sme tento drót naroynali, t. j. urobili by sme z neho usecku; odmerali by sme ju a uloha by bola yyrieśena.

Tento postup nemożno vśak sledovat matematicky, preto ,,narov-nanie“ (cudzim slovom rektifikovanie) obluka musime urobit inac. I. Yśinmime si spósob, akym konstrukcne rektifikujeme obluk,

który je narysovany (napr. obluk AB na obr. 40); pritom obluk AB nemusi byt kruhovym oblukom, może to byt napr. obluk paraboly

(na obr. 40b). Na obluku AB zvolime za sebou body C_v C₂,..., G_n (na obr. 40ab n = 4) a zostrojime lomenu ciaru AC-fi^.. . ,C_nB.

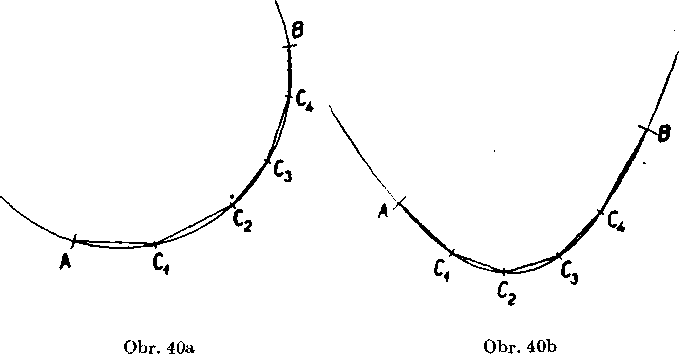
Ak zvolime body C_x, C₂,..., (7_ntak, aby ich pocet n boi dost vel’ky a abyusecky A0₁, C_LC₂,..., G_n-₁C_n, C_n B boli pribliżne rovnako vei’ke (t. j. aby nenastal pripad na obr. 41), lomena ciara AG₁.. .C_nBs& potom mało odliśuje od obluka AB a jej dlżku povażujeme za pribliżnu

dlżku obluka AB.

Tento konśtrukcny spósob możno sledoyat aj poctove. Możno totiż dokazat, że ak pocet stran tejto lomenej ciary neobmedzene yzrasta a dlżka jej najyacśej strany bliżi sa k nule, tvoria dlżky takto yzniknutych lomenych ćiar postupnost, która ma limit. Pritom tento

285