1954 Geometria 270

kład je medzikrużie na obr, 27, t. j. mnożina bodov, ktoró su zvonku krubu Kj o strede S a polomere r_x (a na prislusnej krużnici) a sućasne vo vnutri kruhu K_a o tom istom strede S a polomere r₂ > r_v Medzikrużie doplnime na kruh K₂ kruhom K_x.

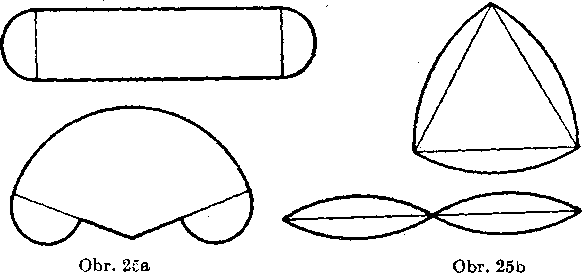
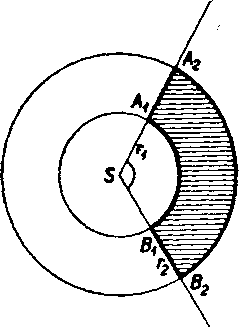
Treti priklad je na obr. 28. Je to vysek medzikrużia, t. j. mnożina bodov spolocnyeh medzikrużiu a uhlu o vrchole v strede S medzikrużia. Vysek medzikrużia doplnime na kruhovy vysek SA_tB₂ vysekom SA_}B_V

Otvary, które só bud zakladnymi obrazeami, bud ich możno doplnif, pripadne rozlożit na zakladne obrazoe, budeme suhrne nazyvat obraz-ce. Pre takto zavedeny pojem obrazea definujeme obsah.

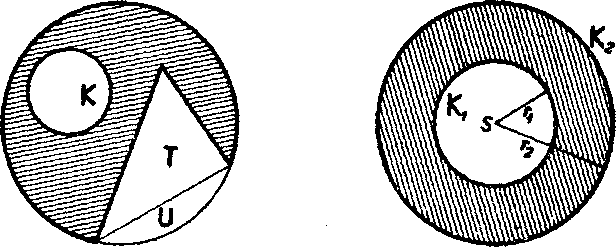
Obr. 26    Obr. 27

Definicia. Obsihom obrazea nazyrame realne óislo, które vyho-vuje tymto podmienkam:

[1]    Obsah obrazea je kladne cislo.

[2]    Obsahy zhodnych' obrazcov sa sebe rovna j u.

[3] Ak sa obrazec O składa z obrazcov Oj, 0₂, ktoró sanavzajom neprekryvaju, obsah obrazea O rovna sa sućtu obsahov obrazcor Oj a 0₂.

Aby sme uroili obsab obrazea jednoznaćne, musime doplnif tri uve-dene podmienky eśte podmienkou [4] z definicie obsahu mnohouholni-ka. Obsah śtvorca, ktoreho strana je jednotkoTa usecka, rovna sa jednej

Poznamky. 1. Z podmienky [3] vyplyva. że obsah każdeho z ohraz-coy O, a 0₂ je menśi neż obsah obraz-ca O (pozri podobnu poznamku na str. 249).

2. Podmienku [3] możno rozśirifi aj na pripad, że obrazec O składa sa z n navzaiom nenrekryvajueich sa casti O^ 0₂, O_n.

Możno dokazaf, że podobne ako v pripade obsahu mnohouholnika (ak priberieme podmienku [4] z definicie). każdy obrazec ma jediny obsah. Tuto votu nebudeme doka-zovat. łba si ćiastocne overime jej platnosf tym, że dokażeme jednozi aćnost obsahu kruhu, kruhovćho vyseku a odseku.

Veta 1. Obsah kruhu o polomere r je

P = k.r*;

pritom konstanta vo rzorei pre obsah kruhu je (fislo, które je vżdy pre rśetky kruhy to iste.

Tuto retu dokażeme tak, że postupne dokażeme keto tvrdenia:

1. Ked postupne zdvojnasobujeme pocet stran pravidelneho K-uhol-nika vpisaneho krużnici k o polomere r, obsahy vzniknutych mnoho-uholnikov tvoria rastucu postupnost, ktoru oznacime

Pn’ Pin’ Pin’ Pgn> Pltn’ •••> Pni^ ’

Pritom podia vzorca (3) na str. 266

. cos

2 R

p « • ^2R i _ = nr² srn —

n

ⁿ    n

kde r je polomer krużnice k.

271