1954 Geometria 234

Bielenie (obr. 90). Nech S_x je stredom vacsej a S₂ stredom mensej podstavy. Lubovol'na rovina co prechadzajuca priamkou 8_X8₂ pretne zrezany kużel’ v liehobeżniku ABGD so zakladnami AB, CI), v ktorom móżeme yykonafi vsetky nase yypocty. Ved’me v royine lichobeżnika

V

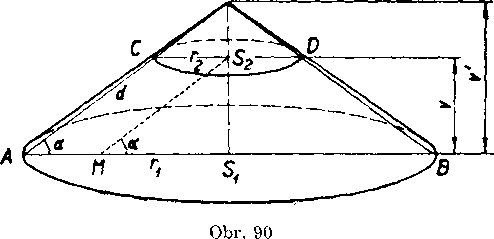
stredom S₂ rovnobeżku s jednym ramenom napr. AD (stranou zreza-neho kużefa). Tym vznikne pravouhly trojuholnik S^^M, z ktoreho

vyplyva sina

8,8.

8₂M

= ~, oc~3Q°52^,,8₁M=]/8₂M²—8^1=20 a z

toho r₂ = 12. Koneene pre Madami vysku kużela v' marne vzfiali

M*

SjM

. Z toho v'

S_XM

24.

Cvićenie

1.    Ake su spolocne utvary vrcholovej roviny a valcoveho (kuże!ove-ho) priestoru, valca (povrchu valca), kużela (povrchu kużela)?

2.    Urcte vsetky roviny sumernosti a) rotacneho valcoveho priestoru, b) rotacneho kuże!oveho priestoru, c) rotacneho valca, d) rotacneho kużela.

3.    Mnożina bodov, które maju od danej priamky s (tzv. osi) tu istu vzdialenost róznu od nuly, je rotacna valcova płocha. Dokażte a vyslovte obdobnu definiciu pre rotacny valcovy priestor.

4.    Je dana priamka s a rovina tz j | s. Akym utvarom je mnożina bodov v ti, które maju od s danu vzdialenost d ^ 0? TJrobte dis-kusiu.

5.    Su dane dve priamky sap. Urcte na p body, które maju od s danu vzdialenosf d ^ 0. Urobte diskusiu.

6.    Mnożina priamok, które prechadzaju danym bodom V priamky s (osi) a maju s ńou tu istu odchylku mensiu neż 90° a vacśiu neż 0°, je rotacna kużel’ova płocka. Dokażte. Vyslovte obdobnu defmiciu pre rotacny kużel’ovy priestor.

7.    V rovine n je dany bod P. I)alej je dany smer p róznobeżny s n. Ved'te v n bodom P priamky, które maju od smeru p danu odchylku. Urobte diskusiu.

8.    Rotacnu valcovu plochu (priestor), rotacnu kużel’ovu plochu (priestor), rotacny yalec a kużel' możno vytvorit otaćanim ur city eh geometrickych utvarov około danej priamky (osi). Udajte tieto utvary a polohu osi.

9.    V elektrostatike poużiva sa kovove teleso (konduktor), które możno vytvorit rotaciou kosouhleho rovnobeżnika około jednej z jeho dlhsich stran. Opisie teleso stereometricky ako utvar, który vzni-kol vhodnym skladanim rotacnych kużel’ov a valca. Udajte prie-seky telesa s rovinami kolmymi na os rotacie.

10.    Ak ma priamka m s plochou a) valcovou, b) kużel’ovou tri rożne body spolocne, je priamkou vrcholovou, a potom ma s plochou TŚetky body spolocne. Dokażte to. Porovnajte s axiómou AII.

11.    Je dany kosy ki obory kużel’.

a)    Urcte, która jeho strana je najyaćśia a która najmenśia.

b)    Polomer riadiacej krużnice je r = 10, vyśka kużela v = 21 a Yzdialenost vrcholu V od stredu S riadiacej krużnice VS = 29. Yypocitajte vel’kost najmensej a najracsej strany.

12.    Dokażte, że nevrcholova rovina rovnobeżna s rovinou riadiacej krużnice pretina kuże!ovy priestor v kruhu.

13.    Definujte rotacny zrezany kużel’, jeho podstavy, vyśku a stranu.

14.    Zobrazte kruhovy valec s podstavami k, k', które leżia v rovinach rovnobeżnych s nakresńou. Stredy krużnic k, k’ oznacte S, 8'. Vo voInej projekcii rieste konstrukcne ulohu:

a)    Danym bodom M' polożte dotykovu rordnu k valcovej płoche.

b)    Zostrojte k valcovej płoche dotykovu rovinu, która je rovno-beżna s danym smerom b. Urobte diskusiu.

5. Gul’ova płocha a gula

Definicia. Mnożina bodov v priestore, które maju tu istu vzdiale-?iost’ r > 0 od daneho bodu 8, vola sa gul’ova płocha. Mnożina bodov, których vżdialenost d od bodu S vyhovuje nerovnostiam 0 ^ d ^ r, vola sa gula.

235