1954 Geometria 022

uhol ma vel'kos£ 90°, preto <£ 613 = 45°. Uhol <t 137 je pociła Taleto-vej vet.y pravy. Preto <£ 1Q3 *= 180° — 45° — 90° = 45°.

Prlklad 2. Ostrouhly trojuholnik ma stred opisanej krużnice vo vnutri trojuholnika, pravouhly trojuholnik na jednej strane (pre-pone), tupouhly trojuholnik zvonku trojuholnika. Dokażte to.

Riesenie. Nech je ACB ostry (obr. 34); pretoźe je to obvodovy uhol (na opisanej kruznici) prisluśny k ureitemu obluku AB, podia poznamky 2 (str. 23) je tento oblók mensi, t. j. stred krużnice 8 leżi

vo vnutri polroviny ABC. Ak su aj ostatne dva uhly <c BAC, <C _CBA ostre, leżi bod S taktież vo rmutri polrorin BCA aj CAB, t. j. vo vnutri trojuholnika ABC.

Ak je uhol <£ ACB pravy, su obidva obluky AB polkrużnice a stra-na AB je priemerom krużnice opisanej. Ak je ACB tupy, je pri-sluśny obluk AB vacśi (pozri pozn. 2 na str. 23), body C, 8 nepatria rnutru tej istej polroviny a bod 8 leżi zvonku trojuholnika ABC.

Cvicenie

1.    Zostrojte dotyćnice krużnice rovnobeżne s danou priamkou. Ved’tę ku krużnici dotycnice z bodu mimo krużnice.

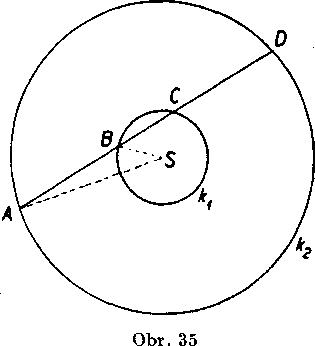
2.    Obr. 35. Krużnice Ic_v k₂ maju spolocny stred S a o polomeroch plati nerovnost r₂ > 3^. Dokażte, że nemożno viest spolocnu sećnu ABCD tak, aby platilo AB = BC = CD. Navod: Odhadnite stra-nu AB v trojuholniku ABS a porovnajte ju s usećkou BC.

3.    Krużnice k_v J:₂ maju stredi u s = O cm a polomery t\ = 5 cm, r₂ = 3,5 cm. Yypoćitajte polomery vsetkych krużnic, które sa dotykajń oboch krużnic k_v k\, a maju stredy na ich osi.

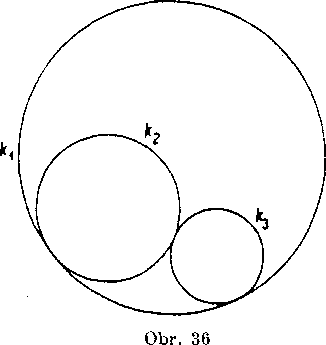
4.    Narysujte obr. 36. Su dane polomery = 6,5 cm, r., = 2 cm, r_z — 3 cm.

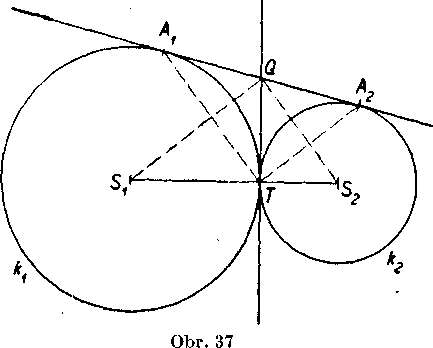
5. Odóvodnite tuto konśtrukciu dotycnlc z bodu A ku krużnici k so stredom S: urcl sa priesecik T usecky AS s krużnicou; ku krużnici Jc zostroji sa dotycnica m v bodę T; na priamke m urcia sa body U, V tak, aby bolo 'SU = S V == SA. Polpriamky SU, SV pretinaju kruźnicu Jc v bodoch dotyku dotycnic, vedenych z bodu A ku krużnici Jc.

23