1954 Geometria 242

południka s povrchom Zenie). Rovina miestneho południka ńliesta A ma od roviny miestneho południka Greenwiche odchylku 15°. Tento stereometricky udaj — aj ked' je doplneny udanim polpriestoru — by vsak nestacil na jednoznacne urcenie południka. Stale eśte existuju dva poludniky, które leżia obidva v udanom (vychodnom) polpriestore a obidva maju od roviny greenwichskeho południka odchylku 15°. Pri udawani zemepisnej dłżky sa preto pouźiva aj suradnic vaćśich neż 90° a zemepisna dlżka sa meria od 0° do 180°. Tymto je potom południk urceny jednoznacne. Keby sme chceli aj stereometricky opisat jednoznacne polohu południka miesta A, museli by sme postupovat asi takto: a) Rovina miestneho południka ma od roviny miestneho południka Greenwiche odchylku 15°; b) południk leżi v polpriestore oddelenom poludnikovou rovinou greenwichskou a obsahujucom bod V na rovniku; c) leżi dalej v polpriestore oddelenom royinou VSZ a obsahujucom bod G (Greenwich).

Obidva póły 8 a J nemaju definovanu zemepisnu dlżku; ich zemepisna śirka sa definuje 90° sev. pre 8 a 90° już. pre J. Aj v tomto pri-pade teda plati, że priamka SOJ ma od roviny rovnika odchylku, która sa rovna zemepisnej sirke bodu 8 (J).

Priklad. Stereometricky odóvodnite, że zemepisnu śirku miesta na severnej pologuli możno urcit meranim vyśky polarky nad obzorom.

Rieśenie. Pripolohe łmezdy polarky stanovime dva predpoklady, które su s dostatocnou presnosfou splnene: a) polarka leżi na zemskej osi (na priamke SJ), b) polarka je nesmierne vzdialena, także spojnica miesta A na povrchu Zeme s polarkou P je priamka AP toho isteho smeru ako SJ.

Rovinou obzoru miesta A volame dotykovu rovinu v bodę A k zemskej guli. Yyskou nejakej hviezdy H nad obzorom volame odchylku, ktoru ma priamka AR od roviny obzoru miesta A. V pripade polarky sa tato odchyłka javi v skutocnej vel’kosti v rovine miestneho południka miesta A. V tejto rovine je narysovany aj obr. 95, v ktorom o znaci priesecriicu roviny obzoru a poludnikovej roviny. Z obrazka ihned vidiet, że vyska polarky nad obzorom sa rovna zemepisnej sirke (severnej) miesta A.

Poznamka o neuklidovskych geometriach

Predstavme si velmi velku gu!ovu plochu, napr. plochu yelkosti naśej Zeme, pripadne eśte omnoho vacśiu. ZvoIme si na nej dva różne body M, N. Pokial priliś neprekrocime obvykle rozmery naśich pracovisk, body M, N uróite nebudu leżat na tom istom priemere, a preto urcuju

jędrni hlavnu rovinu, a teda aj jedinu hlavnu kruznicu na nasej płoche. Z tej to hlavnej krużnice budeme, pravda, pozorovat len malu east a nebudeme mat moźnost odliśit ju od ćasti priamky urcenej bodmi M, N. Budeme preto ochotni povażovat ju za ćast priamky, a to najma preto, że ma yyznacnu vlastnosf priamky udanu axiómou AI. Ak p    zavedieme este ostatne planimetrie-

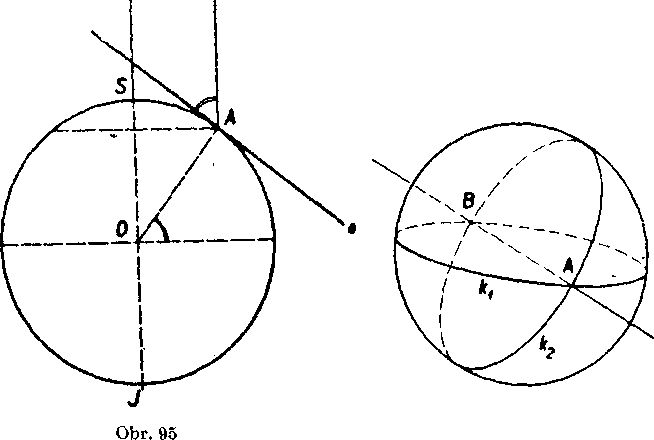
Obr. 96

ke axiómy, móżeme vybudovat geo-metriu, nie vsak v rovine, leż na gu!ovej płoche. Tato geometria budę poużivat miesto priamok hlavne krużnice a budę v mnohych svojich pouckach vel’mi obdobna planimetrii, a to najma v tych, które su odvodcnć z rovnakych axióm.

V niektórych zasadnych veciach budę vsak rozdiel. Prvy z nich, na który narazime, je skutocnost, że v geometrii na gul’ovej płoche nie su rovnobeżky. Skutocne sa każde dve hlavne krużnice k_v k₂ (od seba różne) pretinaju, a to dokonca vo dvoch bodoch A, B (obr. 96). V geometrii na gul’ovej płoche nebude teda platit axióma AV — znamy piaty Euklidov postulat — a budę nahradena axiómou: Każde dve ,,priamky“ sa pretinaju.

Yśetky poucky, które sme dokazovali poużitim axiómy A V, budu zniet inac. Geometria, v której neplati Euklidova axióma A V, vola sa necuklidorska na rozdiel od euklidovskej geometrie, s ktorou ste sa oboznamovali aż doteraz. Nas priklad ukazuje, że neeuklidovska geometria je celkom dobre można — pravda na guIovej płoche.

243