1954 Geometria 150

huje priamku p, lebo inak by priamky p, q leżali v rovine ą neboli by mimobeżne. Rovina A'AG' pretne priamku p v urcitom bodę V, którym musi precbadzafi hladana priecka r. Je teda r = A'V. Prie-sećik U priamok r. q je tym urceny.

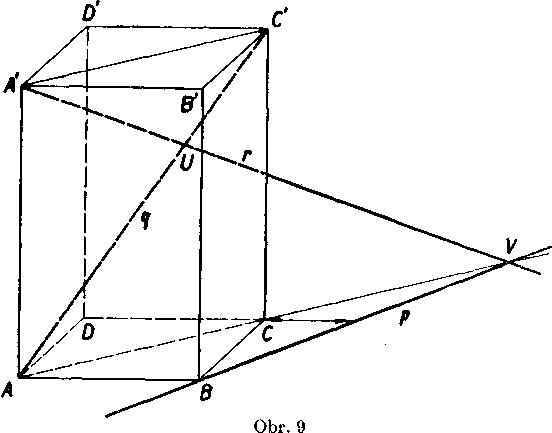
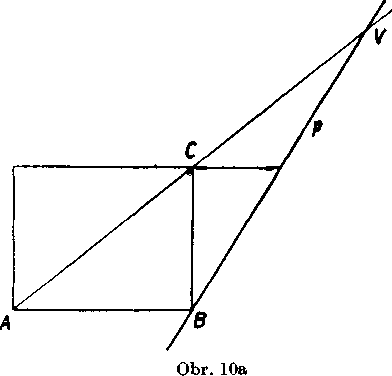
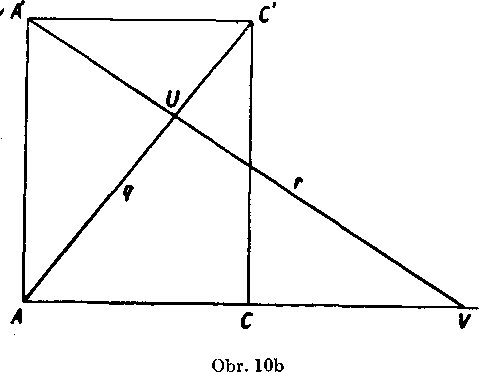
b)Konśtrukciu urobi me vo vol’nej pro-jekcii (obr. 9) postupne v niekolkych ro-vinach (obr. lOab):

V rovine ABC zostrojime obdlżnik ABCD, narysuj eme priamku p = s BX, uhlopriecku AC a zistime bod V = AC .p. Q

V rovine AA 'C zostrojime obdlżnik AC C'A' (dokaż, że tento rovnobeż-nik je obdlżnik, urobime neskór na str. 157). Na priamke AC zostrojime bod V prenesenim z pre-dośleho obrazka, narysu-jeme priamku A'V a zi-stime bod U na priamke AC. Tym dostaneme usecku U V v skutoc-nej vel’kosti.

c)    Dókaz konśtrukcie netreba v tomto pripade robić, lebo jej spravnost je zrejma.

d)    Diskusia. Ul oh a je rieśitelna a ma jedine riesenie, ak su splnene tieto dve podmienky:

(1)    ’Rovina AA'C pretne priamku p (vznikne bod F):

(2)    priamka A'V nie je rovnobeżna s AC'.

Prva podmienka jesplnenavżdy, ked’ je p = p_v kde p_l znaci rovno-beżku s priamkou AC vedenou bodom B. Druha podmienka je splnena vźdy, ked’ je p = p₂) pritom p₂ znaci priamku BX, kde X je priesecik priamok AC, r' a r' je roynobeżka s priamkou AC vedena bodom A'.

Priklad 5a (obr. 11). Body A, B, C povażujte za obrazy (vo vol’nom rovnobeżnom premietani) troch susednych vrcholov pravidelneho sesluholnika ABCDEF v rovine ABC. Narysuj te obraz śestuholnika.

Riesenie. V pravidelnom śestuholniku o strede S (obr. 12) je śtvoruholnik ABCS kosośtvorcom. Yo vol’nom rovnobeźnom premietani obrazom tohto kosostvorca budę rovnobeżnik, także obraz bodu S najdeme z podmienok ob$' || BC, AB || SC. Obrazy dalsich vrcholov śestuholnika konśtruujeme na zaklade vzfahov AS = ST), BS = SE, CS = SF.

151