1954 Geometria 078

Je teda

plati

lebo

tg52°34' = 1,3064; 1,3032 < 1,3064 < 1,3111, 52° 30' < 52° 34' < 52° 40'.

Tento postup volame interpol&ciou a je ufahceny tym, że desatina rozdielu dvoeh susednych hodnót je uvedena v osobitnom stlpei v tabulke (v naśom pripade je to cislo 0,0079).

Priklad 7. Dane je tg a ~ 0,9412; marne urcit x.

Riesenie. V tabulke najdeme

0,9380 = tg 43°10',    0,9435 = tg 43°20'.

Vypocitanie

tga — tg 43°10' = 0,0032.

Pretoże na 1' pripada podrą tabuliek rozdiel 0,00055, pripada rozdiel 0,0032 pribliżne na 6', lebo 0,0032 : 0.00055 = 320 : 55 == 6. Je teda <x 43° 16'.

Priklad 8. Overme si spravnost yzorca (3) pre x = 4°, 7° 30',

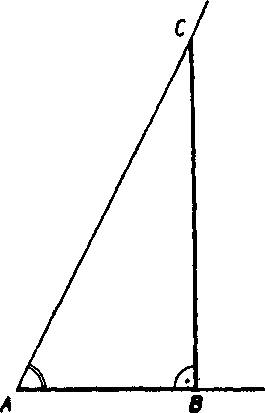
Obr. 93

Obr. 92

Rieśenie. Z tabuliek dostavame:

tg4° == 0,0699; tg 7°30' = 0,1317; tgll° = 0,1944; tgl4^b == 0,2493.

Sucin 0,0175 .« nadobuda v jednotliyych pripadoch hodnoty:

0,0700;    0,1313;    0,1925;    .0,2450.

Vo yśetkych pripadoch suhlasia teda obidva yysledky na 2 desatin-ne miesta.

Ak vieme najst podia tabulky k danej yelkosti uhla hodnotu tan-gens a obratene k danej hodnote tangens vel’kost uhla, móżeme urćo-vat yclkost narysovaneho uhla aj zostrojovat uhol danej yelkosti bez uhlomeru, a to omnoho presnejśie.

Priklad 9. Mamę zistit bez uhlomeru yelkost ostreho uhla KLM z obr. 92.

Riesenie. Na rameno LK nanesieme hoci aj 1 dm; dostaneme bod XJ. Vedieme nim kolmicu k priamke KL a urcime priesecik V priamok KL, LM. Zmeriame usecku UV a jej ve!kost vyjadrime v dm. V na-som pripade je

■ TJ V = 0,685 dm.

Je zrejme

UV

tg^C KLM = -yjt = 0,685.

Łu

V tabulke zistime

tg 34°20' = 0,6830 < 0,685 < 0,6873 = tg 34°30';

je teda

34°20'< <£ KLM < 34°30'.

Uhlomerom by sme veIkos£ uhla s touto presnostou nemohli urcit. Priklad 10. Mamę zostrojit bez uhlomeru uhol 62° 15'.

Rieśenie. Z tabulky vypoćitame

tg 62°15' = 1,8957.

Zostrojime usecku AB o veIkosti hoci aj 1 dm (obr. 93); bodom B ve-dieme kolmicu k priamke AB a nanesieme na ńu usecku yelkosti 1,8957 dm == 1 dm 8 cm 9,5 mm; takto dostaneme bod C.

Uhol <£ CAB ma danu veIkos< 62° 15'.

Poznamka. Trojuholniky na obr. 92, 93 nie su v uSebnici v sku-toćnej yelkosti.

Pomocou tabulky hodnót tangens móżeme rieśit niektóre ulohy o prayouhlom trojuholniku.

*79