1954 Geometria 124

je jej stred bod S_v Eubovolny bod A₁ krużnice k_x prejde do jedneho z bodov A₂, A₂' krużnice k₂, ktoró leżia na priamke S₁A₁. Takto dosta-

vame dve roynolahlosti so stredom 8_X as koeficientami ±    , które

^ri

podia vvsledku prikladu 8 skutocne prevadzaju krużnicu k_x do krużnice k₂.

b) Ak su krużnice k_x, k₂ nesustredne, zvo!me oznaóenie krużnic tak, aby bolo r₂ < r_v Podia vysledku prikladu 8 leżi potom stred hladanej rovnoIahlosti na priamke S_XS₂. Pretoże absolutna hodnota koeficienta rovnoIahlosti je —, musi mat stred rovnoIahlosti od bodov S₂, S_x

^ri

jp

vzdialenosti, które su v pomere —. Taketo body su na priamke S_XS₂

^ri

dva, ako vieme z prikladu 6; jeden z nich J (obr. 143) leżi medzi bodmi S_XS₂, druhy E leżi na prediżeni usećky S_XS₂ za bod S₂. Body E, J móżeme zostrojif podia prikladu 6. Zostrojenie znazornuje obr. 143.

T    Ta

Roynolahlosti so stredmi E, J a s koeficientami —.--- skutocne

r_x    r_x

prevadzaju krużnicu k_x do k₂.

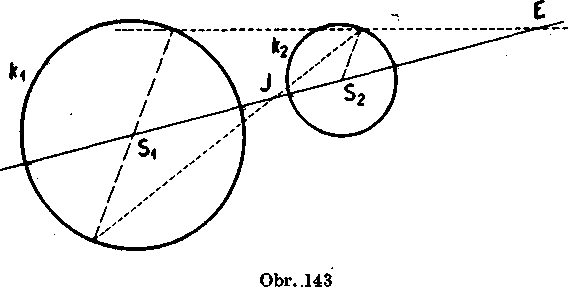
Bod E volame vonkaj§im stredom rovnorahlosti krużnic k_v k_s, bod J vnutornym stredom roynolahlosti krużnic k_x, k₂.

Pomocou stredov roynolahlosti dvoch krużnic vyrie§ime lilohu: Viesf ku dvom nesustrednym krużniciam spolocne dotycnice. Pritom spoloćnou dotyćnicou dvoch krużnic rozumieme priamku, która je dotyćnicou prrej aj druhej krużnice,

Priklad 10. Dane su krużnice k_x s (8_V 40 mm), k₂ = (8_a, 20 mm); ve!kost strednej je S_XS₂ = 52 mm. Marne viesf spolocne dotycnice oboch krużnic.

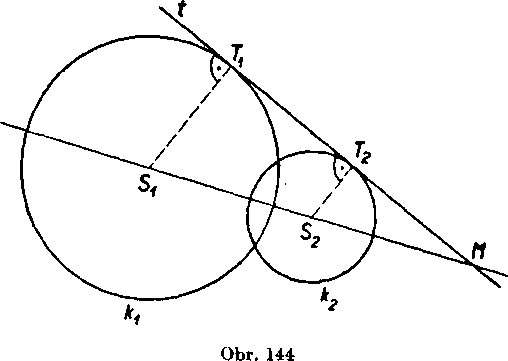
Rieśenie. Pretoźe plati

■r_x — r₂< S_XS₂ < r_x + r₂,

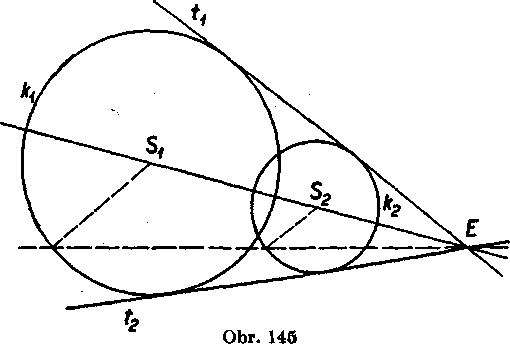
pretinaju sa krużnice k_v k₂ vo dvoch bodoch. Z nazoru je jasne, że krużnice maju dve spolocne dotycnice. Toto odóvodnime aj usudkom. Nech je t spolocnou dotyćnicou krużnic k_x, k₂ (obr. 144) a T_v T₂ jej

125