1954 Geometria 090

1

1

<* > 8, je —— < -Js, ciże cotg a < cotg B. Pretoże funkcia tan-' tg* tg/?

gens nadobuda vsetky kladne hodnoty, to iste plati aj o kotangente. Priebeh funkcie kotangens znazorńuje graf na obr. 106.

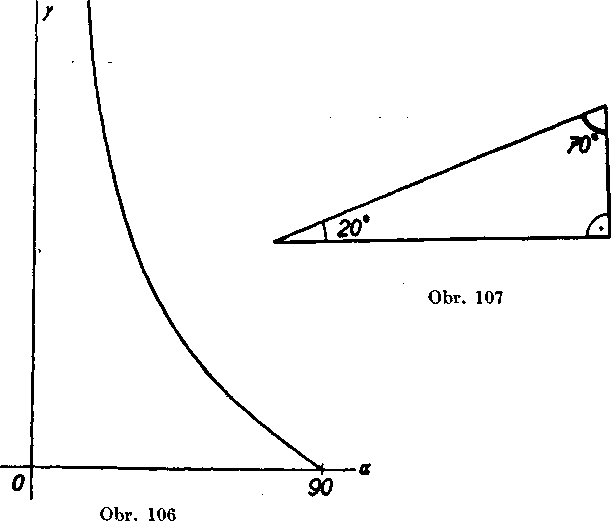
Hodnoty funkcii sinus, kosinus a kotangens su zostavene do tabu-liek podobne ako hodnoty funkcie tangens. Vśimnite si, że każde cislo v tabulkach je bud’ hodnotóu sinusu a sućasne kosinusu, bud’ hod-notou funkcie tangens a sucasne funkcie kotangens. Napr. sin 20° = = cos70°=i;0,3420; obr. 107naspresvedęi, żeskutocnesin20° = cos70°. Pracu s tabułkami ukażeme na dvoch prikladoch.

Priklad 16. Mamę urcit cos 50°32'.

Rieśenie. V tabulke najdeme

cos 50°30' = 0,6361, cos 50°40'= 0,6338.

Rozdiel pripądajuci na 10' je 0,0023; urobime interpolaciu podobne ako pri funkcii tangens (pr. 6, str, 77). Na 1/ pripadne rozdiel 0,00023, na 2' asi 0,0005. Tuto opravu odcitame od cos 50°30', pretoże ko-sinus sa zmensuje, ked’ uhol rastie. Preto je

cos 50° 32' = 0,6356.

Priklad 17. Je dane cotg a = 1,3862. Mamę urcit yelkosf uhla «. Rieśenie . V tabulke yyhladame

cotg 35°40' = 1,3934, cotg 35°50' = 1,3846.

Vypoćit.ame rozdiel cotg 35°40' — cotg oc = 0,0072. Na 10' pripada rozdiel 0,0086; 0,0072 pripada teda asi na 8'. HIadana yelkosf je

x== 35°48'.

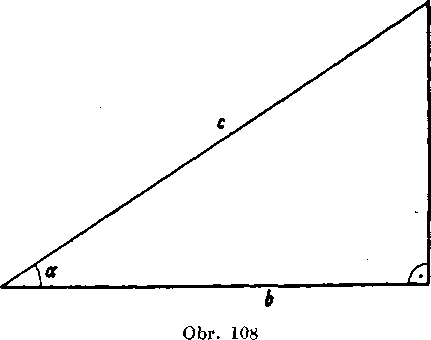
Na niekolkych prikladoch ukaże-me, ako poużijeme goniometricke funkcie na rieśenie uloh o prayouhlom troj-uholniku.

Priklad 18.Pra-youhly trojuholnik ma odyesnu a = = 9,2 cm apreponu c = 14,7 cm. Urcte yypoctom zvyśnu stranu a ysetky uhly.

Rieśenie (obr. 108). Urcime najskór uhol a, leżiaci oproti odvesne a. Plati

9,2

14,7-

a

sm x — — c

Pomocou tabulky obratenych cisel dostaneme

sin x ~ 0,6259

a z tabulky hodnót sinusu dostaneme a = 38°45'.

Całej je

cotg a =

b_

a

91