1954 Geometria 120

5.    Je dany duty uhol *£PQR a b.od S, który leżi vo vnutri uhla. Zostrojte rovnoramenny trojuholnik SXY tak, aby bod X leżał na polpriamke QP, bod Y na polpriamke QR a aby platilo YX — YS, YX X QR- Nayod: Poużite rovno!ahlost o strede Q.

6.    Dane su dve róznobeżky a, b a bod H, który neleżł ani na jednej z nich. Urcte bod Z na priamke a tak, aby boi od bodu H rovnako yzdialeny ako od priamky b. Navod: Poużite yysledok cvicenia 5.

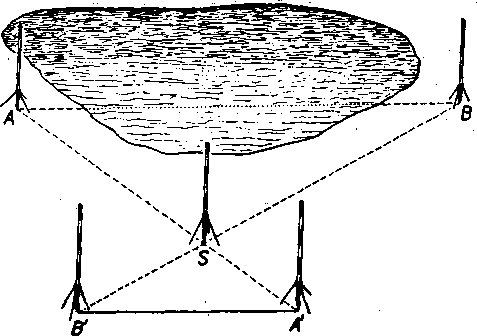
Obr. 138

7.

V terene mamę zistif vzdialenost dvoch bodov A, B, medzi którymi je prekażka. Zvolime bod 8, vytycime priamky AS, BS, zmeriame usecky AS, BS a podia obr. 138 vytyćime body A', B’ tak, aby bolo A’S = IcAS, B'8 — kBS, kde k je IubovoIne kladne cislo (obycajne

k< 1). Potom zmeriame usecku A’B’ a rypoeitame AB — -p4 'S'.

Odóvodnite tento postup a preved’te ho v terene.

3. Krużnica v roynolahlosti

Priklad 8. Je dana rovnoIahlosf o strede S as koeficientom X a dalej krużnica k = (O; r). M&me zośtrojif utvar, który je rovnoIahly s kruż-nicou k podia stredu S.    '

5

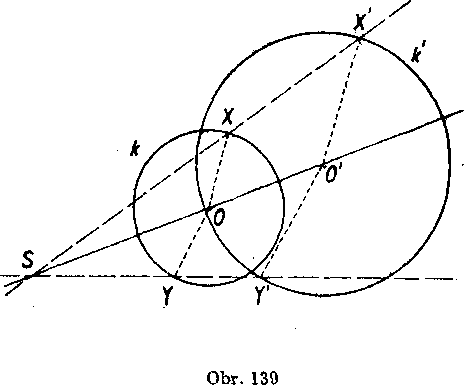
Rieśenie. (Obr. 139). Urcime obraz 0' bodu O (na obr. 139 je ■£=—)

O

a opiżeme krużnicu ¥ so stredom 0' a polomerom r' = | A |.r. Eahko dokażeme, że krużnica ¥ je obrazom krużnice k.

Nech je X IubovoIny bod krużnice k (obr. 139). Pre jeho obraz X' plati podia vety 1

0'X' = |A| .OX= jA j.r = r';

bod X' teda leżi na krużnici ¥. Nech je Y' Tuboyolny bod krużnice ¥ (obr. 139). RovnoIahlosf so stredom 8 as koeficientom — preva-dza bod Y' do bodu Y, pre który plati

^{0r =} Pl °'^r' ^{=    = n}

bod P leżi teda na krużnici k; bod Y' je obrazom bodu Y v rovno-lahlosti so stredom Sas koeficientom A.

Dokazali sme teda: Każdy bod krużnice k ma svoj obraz na krużnici ¥ a obratene każdy bod krużnice ¥ ]e obrazom niektoreho bodu krużnice k. Vysledok móżeme povedat takto:

RovnoIahlost prevadza krużnicu k do krużnice ¥; stred krużnice ¥ je obrazom stredu krużnice k a polomer krużnice ¥ je sużin polomeru krużnice k a absolutnej, hodnoty koeficienta rovnoIahlosti.

121