1954 Geometria 190

Cvicenie

1.    Dokażte;

a)    Ak je A bod, p priamka, d yzdialenost bodu A od priamky p a X Iubovol’ny bod na p, plati AX N d. Kędy plati znamienko rovnosti?

b)    Ak je A bod, q rovina, d yzdialenost bodu A od roviny o a. X 1’uboyolny bod v q, plati AX A d. Kędy plati znamienko rov-nosti ?

2.    Preco musia byt vo vetach 25 a 26 body A_v A_z, resp. A_x, A₂, A₃ v jednom polpriestore, który je oddeleny rovinou? Udajte priklad, który ukaże, że vety bez tej to podmienky by neboli spravne.

3.    Urcte mnożinu bodov, które maju od danej roviny danu yzdiale-nosf.

4.    Je dana kocka ABGDA'B'G'D' y zakladnej polohe. M je stredom usecky AB, N stredom usecky GD. tJrcte konstrukcne vzdiale-nost priamky A'D' od roviny MNB’. Nech je P Iubovol’nym bodom priamky A'D' a PQ jeho vzdialenosf od roviny MNB'; dokażte, że pomer vzdialenosti bodu Q od royiny A'B'C' a od roviny ABC je 2 : 3.

5.    Dokażte, że mnożina bodov, które maju rovnaku yzdialenost od danych dvoch różnych bodov A, B, je rovina kolma na priamku AB, prechadzajuca stredom usecky AB. Navod: poużite postup znamy z planimetrie.

6.    Dokażte: Mnożina bodoy, które maju rovnake yzdialenosti od troch danych bodov A, B, G, neleżiacich na jednej priamke, je priamka kolma na rovinu ABC a prechadza stredom krużnice opisanej trojuholniku ABC.

7.    Ak su A, B, C, D styri body neleżiace v jednej rovine, existuje jediny bod, który ma od yśetkych śtyroch bodov tu istu yzdiale-nosf. Dokażte a udajte konstrukciu.

8. V styorstene ABGD oznacme D', G", B', A' po poriadku stredy krużnic, które su opisane trojuholnikom ABC, ABD, AGD, BCD a oznacme d, c, b, a kolmice vedene po poriadku tymito bodmi na royiny trojuholnikoy; vsetky styri priamky a, b, c, d precha-dzaju jednym bodom; dokażte na zaklade cvićenia 7.

9.    Su dane dva różne body A, B a priamka p (rovina q). Najdite yśetky body priamky p (royiny q), które su rovnako yzdialene od A aj od B. Urobte diskusiu.

/f(3) Urcte mnożinu bodov, które maju yzdialenost d_x od royiny o a d., od royiny a. Urobte diskusiu.

11). Dane su dve usecky AB. OD. Urcte mnożinu bodoy, które maj u rovnaku yzdialenost od bodov A a B a aj rovnaku yzdialenost (pravda, nie vżdy tu istu ako v predoślom pripade) od bodov C a D. Urobte diskusiu a v każdom pripade, ked hladana mnożina yznikne, urcte vztah ziskaneho utyaru k priamkam AB, CD.

12.    Dokażte existenciu telesa, które je obmedzene śiestimi zhodnymi śtyorcami a dvoma prayidelnymi sesfuholnikmi. Zobrazte teleso vo yolnom rovnobeżnom premietani tak, aby dva zo stvorcov boli roynobeżne s nakresńou. Oznacte ABCDEF a A'B'C'D'E'F' obidya sestuholniky; oznaóenie vrcholov zvol’te tak, aby ABB'A' boi stvorec leżiaci v rovine rovnobeżnej s nakresnou. Zobrazte uzavretii lpmenu ciaru, v której teleso pretina rovina AC'E₀, kde E₀ je stredom usecky EE'.

13.    Su dane dye kolme priamky p a q. Ćo yyplni priamka q, ak ju ota-came około priamky p ako osi? Uvażujte o pripade, ked

a)    p a q su mimobeżky,

b)    p a q su róznobeżky.

4. Sumernost podia royiny

V planimetrii ste poznali różne zobrazenia. Najdóleżitejśim zobra-zenim bola sumernost podia osi. Aj y priestore możno definovat mnoho ^ geometrickych zobrazeni; v tom-to clanku sa obmedzime na naj-dóleżitejsie z nich, na sumernost podia royiny (rovinovu sumernost) , ktora’ma obdobne ylastnosti ako sumernost osoya v rovine.

Definicia. Nech je dana rovi-na n, nazyyana royina sumenicsti.

K l’ubovoInemu bodu X v priestore urcme obraz podia tohto navo-du:

a)    Ak leżi bod X v rovine n, je X' = X.

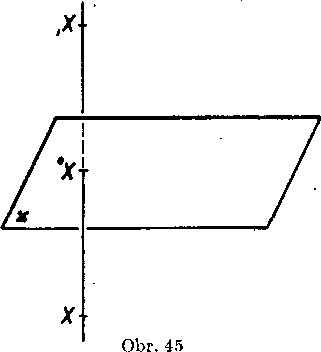
b)    Ak neleżi bod X v rovine n, oznacme X₀patu kolmice yedenej bodom X na rovinu n. Obraz X' potom leżi na predlżeni usecky XX₀ za bod X₀ tak; że XX₀ = X₀X' (obr. 45).

Zobrazenie urcene tymto sposobom nazyyame rovinova sumernost (sumernost podia royiny n).

191