1954 Geometria 222

ky ihlanoyeho priestoru su vnutornymi priamkami ihlanoveho priesto-ru a vypł na ju vnutro ihlanoveho priestoru. Bod V vśak nepocitame do vnutra ihlanoyeho priestoru.

Priamkyihlanovejpłochy,któreprechadzaju vrcholmi A_1} A₂,...,A_n riadiaceho mnohouholnika, yolaju sa boćne hrany. Ak je n poćet hran

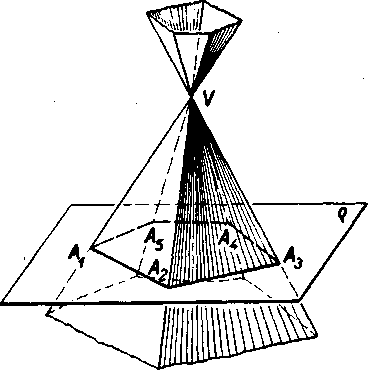
ihlanovej płochy, vola sa ihla-nova płocha n-boka a aj ihlano-vy priestor je w-boky. Hrany, które prechadzaju dvoma su-sednymi vrcholmi riadiaceho trojuholnika, su susednymi hranami. Mnoźina priamok ihla-novej płochy, które pretinaju tu istu stranu riadiaceho mnohouholnika, tvori stenu ihlanovej płochy. Steny su dvojice vrcho-lovych uhlov o vrchole V a je ich prave tolko ako hran.

Obr. 79

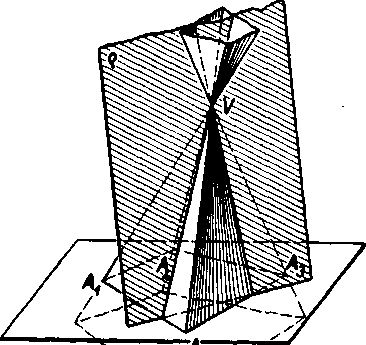
Każda priamka ihlanoveho priestoru je bodom V rozdelena na dve polpriamky. Polpriam-ky, które prechadzaju bodmi riadiaceho mnohouholnika, vy-plńaju ćast ihlanoYeho priestoru, która sa nazyva cast pri-1'ahla k riadiacemu mnohouhol-niku.

Aj preihlanovy priestor możno vysloYit Yety obdobne ve-te 34.

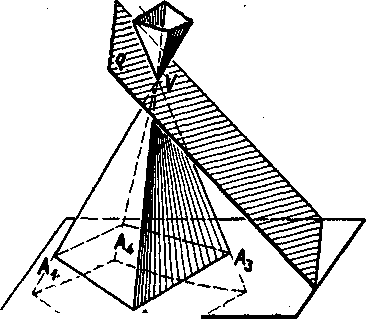
Veta 36. Cast a-hokeho ihla-noveho priestoru, prilahla k riadiacemu mnohouholniku, je spolocnym utvarom n polprie-storov. Zvysna cast ihlanoyeho priestoru doplnena yrcholom V je spolocnym utvarom opacnych n polpriestoroy.

Vety nebudeme dokazovat. Ilustraciu podava obr. 79.

Obr. 80a

Priamky, które prechadzaju yrcholom V, volameYrcholovy-

mi priamkami. Vrcholova priamka ma s ihlanovym priestorom społocny iba vrchol V alebo prislucha ihlanovemu priestoru. V druhom pripade je to bud’ ynutorna priamka, bud’ priamka ihlanovej płochy, pripadne niektóra, z hran.

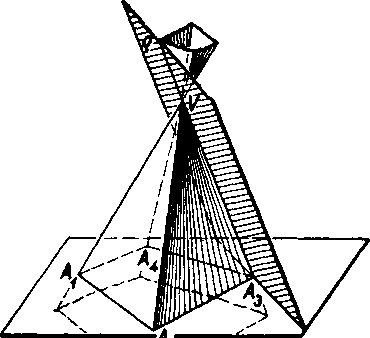
Roviny, które prechadzaju yrcholom F, volame yrcholo-vymi rovinami.

Vrcholova rovina ma s ihla-novou plochou spolocnu bud’ nekonecnu mnożinu priamok, ak obsahuje stenu ihlanovej płochy, bud’ dve różne yrcholo-ve priamky, bud’ jedinu yrcho-lovu priamku, a to hranu, bud’ iba vrchol V (obr. 80a, b, c).

Skór neż vyslovime a doka-żeme yetu obdobnu vete 35, musime rozsirit pojem podob-nosti obrazcov na dva obrazce leżiace v różnych rovinach. De-finujeme:

Obr. 80b

Nech su dane dva rovinne obrazce U, U_x leżiace v rovi-nAch q,a. Premiestime akukol-vek rovinu a do roviny q; tym prejde obrazec U_x do urciteho obrazca U', który je zhodny s U_x. Ak su obrazce U, U', które leżia v tejże royine q, podobne (y planimetrickom zmyśle), nazyyame aj obrazce U,

U_x podobnymi.

Rovina, która nie je vrcho-lova a nie je ani rovnobeżna so żiadnou vrcholovou priamkou ihlanoyeho priestoru, ma s ihla-novym w-bokym priestorom społocny yypukly n-uholnik (tzv. priesek roviny a ihlano-veho priestoru).

Obr 80c

Z 9. rocnika vieme, że naj-jednoduchSim pripadom po-

223