1954 Geometria 198

Definicia. Dva utvary V a V' y priestore volame zhodnymi vte-dy, ak możno najst konecny pocet rovinovych sumernosti tak, że ak zobrazime utvar V prvou sumernostou, vzniknuty obraz ^XV dru-hou sumernostou, novy obraz ²V trefou sumernostou atd’., je V obrazom v poslednej rovinovej sumernosti.

Po tej to defimcii vsak vznika pochybnost, ći nemame pre rovinne utvary umiestene v priestore dvojaku zhodnost, a to jednak zhodnost v smysle prave definovanom v priestore, jednak zhodnost v starom zmyśle, ako bola zavedena v cl. 1. Móżeme dokazat, że to tak nie je; dokaż nebudeme robit. Na ukążku uvedieme jednoduchy priklad.

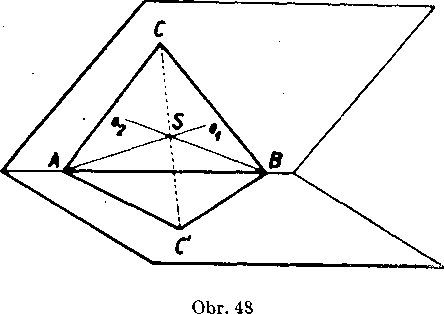
Priklad 10. Su dane dva trojuholniky ABC, ABC' leżiace v różnych rovinach. O ich stranach plati AC = AC", BC = BC. Marne dokazat, że rovinovymi sumernostami możno previest trojuholnik ABC v trojuholnik ABC.

Rieśenie (obr. 48). Z predpokladov vyplyva, że obidva trojuhol-niky su zhodne podia vety sss ako rovinne utvary. Marne dokazat, że su zhodne aj podia novej definicie.

Oznacme o_Ł os usecky CC' , która leżi v rovine ACC’. Podia znamej vety z planimetrie os o_x prechadza bodom A, stredom S usecky CC' a je Oj J_ CC. Oznacme o₂ os usecky CC', która leżi v rovine BCC’; priamka o₂ prechadza bodom B, bodom S a je o₂ J_ CC'. Priamky Oj, o₂ nesplynu, pretoże v opacnom pripade by leżali vśetky śtyri body A, B, C, C v rovine, ćo odporuje predpokladu. Priamky o_1; o₂, które maju spoloćny bod 8, su teda róznobeżne a ich rovina o je podia vety kolma na priamku CC. Sumernost podia roviny q prevedie teda body A, B, C po poriadku v body A, B, C'\ tym je naśe tvrdenie dokazane.

Pretoźe zhodnost v priestore zahrńuje v sebe zhodnost v rovine, móżeme aj v priestore poużivat ten isty symbol > ako predtym; niet obayy, że vznikne nedorozumenie.

V planimetrii si każdu zhodnost móżeme predstavit ako premieste-nie. V stereometrii tomu tak nie je, ako sme sa uż zmienili. Bez zacha-dzania do podrobnosti, ukażeme na prikladoch, że'v priestore sa vy-skytuje dvojaka zhodnost. Priamo zhodne su take dva ńtvary, które

sa móżu yhodnym premiestenim stotożnit, pritom vśak predpoklada-me, że ide len o geometricke utvary, a nie o utvary hmotne, napr. telesa zo skutocneho materiału, kde stotożnenie nie je możne pre ne-priestupnost hmoty. Nepriamo zhodne su take utvary, które su sice zhodne podia definicie zhodnosti, nemożno ich vśak stotożnit premiestenim.

Priklady. Dve kocky, których hrany su zhodne, dve gule o rov-nakych polomeroch su priamo zhodne. Ten isty pojem prenasame potom aj na hmotne predmety, aj ked’ ich prakticky nemóżeme sto-toźnit. Tak su napr. dve desathalierove mince priamo zhodne (ak si odmyslime neodstranitelne mikroskopicke nepresnosti, które vznikli pri vyrobe alebo inym sposobom).

Naproti tomu niektóre ine vyrobky różnych odvetvi priemyslu sa móżu vyskytovat aj ako pary utvarov nepriamo zhodnych. Napr. prava a Iava rukavica, prava a l’ava topanka toho isteho paru. Iny znamy priklad je pravotociva a Iavotociva skrutka rovnakych roz-merov.

Ine predmety — najma nastroje — sa vyrabaju len v jednej podo-be, urcenej na poużivanie iba urcitym sposobom. Nepriamo zhodny variant, który by vyżadoval poużitie druhej ruky alebo obratene po-stavenie obidvoch ruk, by boi menej • pohodlny a nevyraba sa. Pri-kladom je kosa, ktoru możno uchopit a poużivat len jednym sposobom. Ine priklady su zlievacska lyżica (obr. 49), skrabacka na zemiaky, śijaci strój a i.

199