1954 Geometria 240

(3) maju spolocne dva różne body X, Y, sumerne polożene vzhIadom na os S_X8_Z. V tomto pripade su spolocne body obidvoch krużnic vrchol-mi trojuholnikov o stranach Sj3_z, r_x, r₂.

Ak vedieme priamkou inu rovinu a, 1’ahko zistime, że v obi-dvoch rovinach q, a nastanę sucasne bud’ pripad (1), bud’ pripad (2), bud' pripad (3). Ak nastanę pripad (3), leżia vsetky styri spo

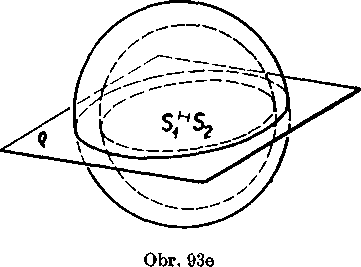
locne body obidvoch gu!ovych plóch v urćitej rovine r, która j e kolma na priamku S_X8_Z a vśet-ky maju od priamky 8_xS_ztxi istu Yzdialenost; toto tvrdenie ne-budeme podrobne odóvodno-va£.

Celkove dostavame teda od-poved:

1. Dve gu!ove płochy móżu byt sustredne a potom maju bud spolocne vsetky body, bud’ ni-jaky, podia toho, ci je r_x = r₂, alebo r_x yfe r₂.

2.    I)ve nesustredne gu!ovś płochy nemaju nijaky spolocny bod, ak je bud’ S_X8_Z > r₁ + r_z, bud’ 8_XS_Z < \r_x — r_z | a r_x ^ r₂.

3.    Dve nesustredne gu!ove płochy maju na spojnici obidvoch stredov spolocny jediny bod (dotykaju sa), ak je bud’ S_X8_Z = r_x + r₂, bud’ 8_X8_Z = | r_x — r₂ j a r_x yŁ r₂. V prvom pripade je spolocny bod vnutor-nym bodom usecky S_XS₂, v druhom leż! na predlżenl tejto usećky za stredom gu!ovej płochy s menslm polomerom.

4.    Dve nesustredne gu!ove płochy sa pretlnaju v krużnici, której rovina je kolma na spojnicu S_XS₂ a której stred leż! na S_XS_Z, tento pripad nastanę, ak je | r_x — r₂ | < 8_X8_Z < r_x + r₂. Podrobne odóvod-nenie nebudeme robit.

Zemepisne aplikacie. Zemsky povrch możno pribliżne povażovat za gu!ovu plochu, która ma polomer R = 6 378 km. Jeden z priemerov tejto guIovej płochy ma yynimocne postavenie. Predlżenie tohto prie-meru je tzv. zemska os; około nej sa Zem pravidelne otocl raz za łmezdny den. Obidva prieseclky osi s povrchom Zeme volaju sa póły (severny a jużny S, J, obr. 94). Każda hlavna rovina, która prechadza osou, vola sa poludnlkova rovina a pretlna povrch Zeme v hlavnej krużnici. Obidve polkrużnice s koncovymi bodmi S, J na tejto krużnici volaju sa poludniky p. Każdym bodom na povrchu Zeme (s yynimkou obidvoch pólov) prechadza jediny południk, pretoże existuje jedina poludnikova rovina prechadzajuca danym bodom.

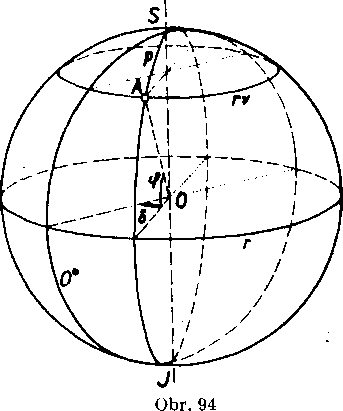
Hlavna rovina kolma na os vola sa rovnikova rovina; poyrch Zeme pretina v hlaynej krużnici, która sa vóla rovnik r a dęli zemsku gul’u na dve pologule, severnu a jużnu. Roviny rovnobeżne a różne od rov-nikovej roviny, pokial’ pretinaju usećku SJ vo ynutornych bodoch, yytinaju na povrchu Zeme ve-dlajśie krużnice, które sa yolaju roynobeżky. Każdym bodom na povrchu Zeme (s vynim-kou pólov) prechadza jedina rovnobeżka, pretoże danym bodom prechadza jedina rovina kolma na SJ; tato rovina pretina usecku SJ vo vnutornom bodę.

Obratene, ak je dany urcity południk a urcita rovnobeżka, je tym urceny jediny bod na povrchu Zeme. Body povrchu Zeme (s vynimkou pólov) a nimi prechadzajuce rovnobeżky, resp. poludnikove polkrużnice, su si tedavz4jomne jednoznac-ne priradene. Tymto je umoż-nene zayedenie zemepisnych suradnic.

Pre zavedenie suradnic je potrebne zyolit zakladne ciary. Yiete zo zemepisu, że pre sustayu rovnobeżiek je zakladnou krużnicou roynik; pre sustayu poludnikoyych polkrużnic (tzv. miestnych poludnikov) móżu byt zakladne ciary różne. Najcastejśie sa yoli miestny południk, który prechadza hvezdarnou v Greenwichi pri Londyne. Viete aj, ako su priradene pri tychto vol’bach rovnobeżky a poludnikoye polkrużnice k cislam.

Co znamena stereometricky udaj, że urcite miesto A zemskeho po-vrchu leżi na 50° severnej sirky a 15° yychodnej dlżky? To znamena, że miesto A leżi v polpriestore, oddelenom rovnikovou rovinou a obsa-hujucom bod S, na rovnobeżke, która je oznacena 50°, co znaci, że priemer O A ma od roynikovej roviny odchylku 50°. I)alej to znamena, że miesto A leżi v polpriestore oddelenom poludnikovou rovinou green-wichskeho miestneho południka a obsahujucom bod V na rovniku (V, Z su prieseciky priemeru kolmeho na rovinu greenwichskeho

241