1954 Geometria 228

I Krużnicu k z predoślej definieie budeme volat riadiaeou krużnicou faIcoveho priestoru alebo valcovej płochy. Valcovy priestor alebo valcova płocha nazyya sa rotacnou, ak je p J_ g.

Poznamky. Obśłrnejśie a presnejśie by sme mali hoyorit o kruho-vom valcovom priestore (płoche), pretoże możno uvażovat aj o inych uzavretych krivkach ako o utvaroch riadiacich. Privlastok kruhovy budeme vsak spravidla vynechavaf .

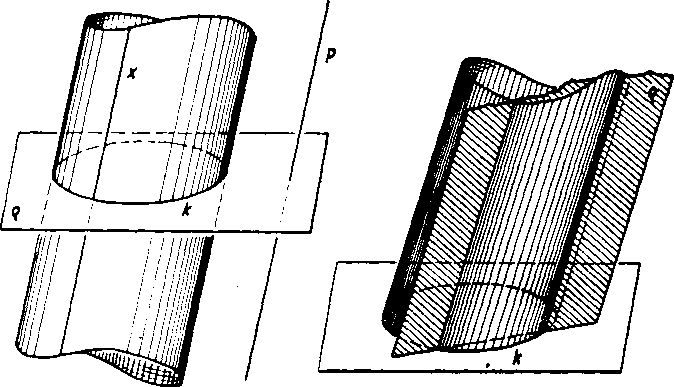
Obr. 83    Obr. 84a

Priestorovy utvar volame rotafinym, ak ho możno vytvori£ otaca-nim (rotaciou) nejakeho rovinneho ńtvaru około danej priamky (osi rotacie). Napr. rotacna valcova płocha vznikne otacanim priamky około inej priamky, która je s ńou rovnobeżna a nesplyvajuca. Rotać-ny valcovy priestor vznikne rotaciou rovinneho pasa około jednej z priamok, które ho ohranicuju.

Priamky valcoveho priestoru, które nie su priamkami valcovej płochy, su priamky vnutorne. Ich body vyplńaju vnutro valcoveho priestoru.

Priamky smeru p budeme volafi tak, ako pri hranoloyom priestore, vrcholovymi priamkami a royiny rovnobeżne s p vrcholovymi ro-yinami.

Yrcholoya rovina ma s valcovou plochou spoloćne bud! dve różne

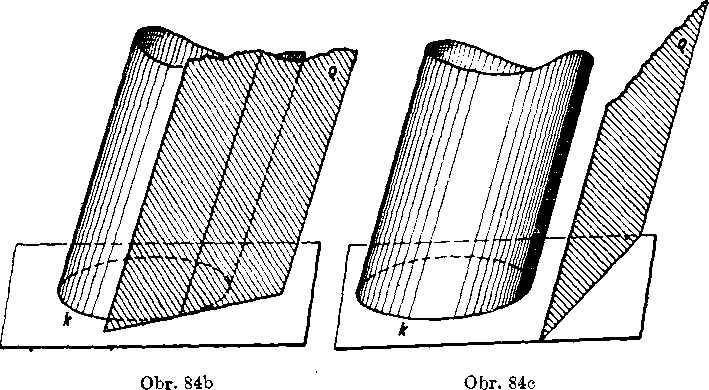
vrcholove priamky (secna rovina), bud’ jednu vrcholovu priamku (dotykova rovina), bud’ s ńou nema spolocny vóbec nijaky bod (nesec-na rovina) (obr. 84abc).

Veta 38. Rovina rovnobeżna s rovinou riadiacej krużnice pretfna vaIcovu plochu v krużnici, która je zhodna s riadiacou krużnicou.

Dokaż (obr. 85): Oznaenie 8 stred riadiacej kruznice, A jej l’ubovoI-ny bod a a rovinu rovnobeżnu s rovinou riadiacej kruznice. Nech je s vrcholova priamka vedena bodom 8, a vrcholova priamka vedena bodom A; oznacme 8' s s.a, A' = a.a. Eahko dokażeme, że śtvor-uholnik 8AA'8' je rovnobeżnik a ze A’ je bodom utvaru K, który je

spolocny valcovej płoche a rovine o. Aj naopak ihned’ Yidiet, że każdy bod utvaru K Yznikne opisanou cestou z urciteho bodu riadiacej kruż-nice. Z to ho vyplyva, że każdy bod utvaru K, który leżi v rovine a, ma od bodu 8' stalu vzdialenost A'8' = AS = r, kde r je polomerom riadiacej krużnice. Utvar K je teda kruźnica, która je zhodna s riadiacou krużnicou.

Teraz budeme definovai dalśie zname teleso, które nazyvame valec.

Definicia. Nech je dany valcovy priestor a dve różne roviny <x, fi rovnobeźne s rovinou jeho riadiacej krużnice. Potom utvar, który je spolocny valcoYÓmu priestoru a vrstve a, fi, volame kruhoYy yalec. TJsecky vytate na priamkach prisluśnej valcovej płochy rovinami «, j? Yolaju sa strany valea.

229