1954 Geometria 232

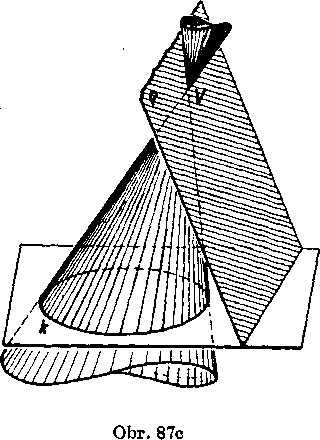
Kużel, który vznikol z rotaćneho kużel’oveho priestoru, je rotaćny kużel’.

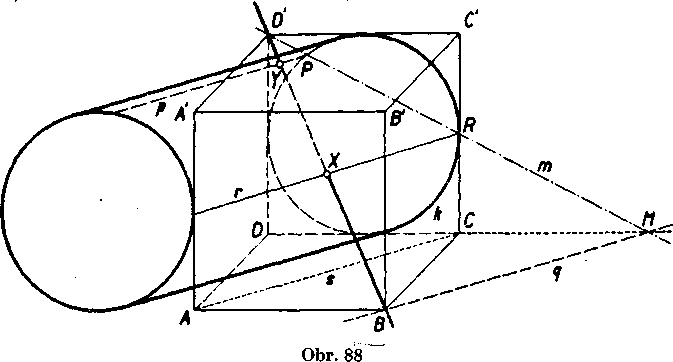
Priklad 4 (obr. 88). Je dana kocka ABGDA 'B'C'D'. Valcova płocha je dana riadiacou krużnicou Jc, ktorś je vpisana do stvorca CDD'C, a smerom p = AC. Urćte priesećłky valcovej płochy a priamky BD'.

Rieśenie. Priamkou BD' vedie-me vrcholovu rovinu a, która je urće-na priainkou BD' a priamkou q\\AC incidentnou s B. Jej priesecnica s ro-vinou CDD'C' riadiacej krużnice je priamka m = AID'. Priesecikmi P, R priamky m s riadiacou krużnicou prechadzaju vrcholove priamky p, q, v których royina a pretina yalcoYU plochu. Na priamkach p, q a priam-ke BD' leżia hladane priesećłky X, Y.

Priklad 5 (obr. 89). Kuźeł’ova płocha ma vrchol v bodę B kvadra ABCDA'B’C'D' a riadiacu krużnicu Ic danu stredom C a polomerom

C'M = — C'D v rovine CCD'. Bod

Pje stredom obdlżnika ADD'A '.Ved-me bodom P dotykove roviny k danej kużelo-rej płoche.

Riesenie. Każda dotykova rovina je yrcholova. HIadane dotykove royiny obsahuju teda priamku FP a ich priesecnice s rovinou riadiacej krużnice preehadzaju bodom R = VP,CO'D. Tieto priesecnice musia v&ak byt dotycnicami riadiacej krużnice. Pretoże z vonkajśieho bodu R możno viest ku krużnici dve dotycnice t, u, ma uloha dve rieSenia. HIadane roviny su tV a uV.

Rovina, która je rovnobeżna s rovinou GC'D podstavy kużela a która pretina strany kużela vo vnutornych bodoch, rozdęli kużel na novy kużel’ a na zrezany kużel’. Podobne ako ypriklade 3 nastr. 225

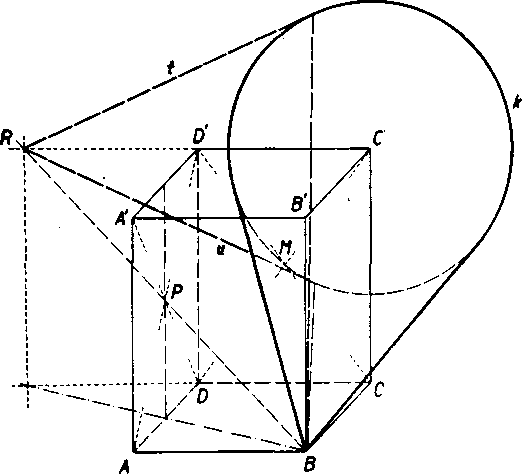
Obr. 89

możno dokazaf, że polomery obidvoch podstay su v tom istom pomere ako vyśky oboch kużeloy. Teraz rozrieśime poctovu ulohu o zrezanom kużeli.

Priklad 6. Je dana, vyśka rotaćneho zrezaneho kużela v = 15, polomer vacśej podstavy r_x = 32 a vel’kost strany zrezaneho kużela d = 25. Vypocitajme a) odchylku strany a podstayy, b) polomer dru-hej podstayy a c) vyśku kużela, który yznikne zo zrezaneho kużela predlżenim stran.

233