1954 Geometria 348

I) l o h a 1. Urcte piast zrezaneho rotaćneho kuźela.

Riesenie. Oznacme polomery podstav daneho zrezaneho kuźela r_x, r₂ (predpokladame r₁ > r₂) a jeho stranu s (obr. 89). Ako vieme, dany

zrezany kuźel móźeme povazovat za rozdiel dvoch rotaćnych kużel’ov, których podstavy maju polomery r_x, r_z. Ak strany tychto kużel’ov su

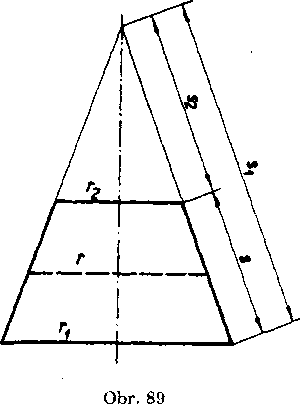
5₁ a -s₂ = s_x — s, plati pre ne ńmera *1 •• ^s2 == ^ri •• r_t;

z toho dostaneme (r_x — r₂ 7Ł 0);

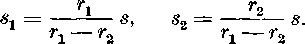
Pretoże plaśt daneho zrezaneho kuźela je rozdielom plaśtov obidvoch zostrojenych kużeloT, dostaneme

7ir₁s₁ — TlTgS₂ =

Poznamka 1. Ak oznacime piast zrezaneho kuźela pismenom p, po-lomery jeho podstav r_v r₂ a stranu s, móżeme vysledok, który sme dostali, vyjadrit yzorcorn

V = ™(^ri + r₂)s.

Poznamka 2. Ak na zrezanom rotacnom kużeli zostrojime stredny rez, t. j. krużnicu, której rovina rozpoluje jeho vyśku a jena ńu kolma

(obr. 89), zistime, że jej polomer sa rovna -i- {r₁ + r₂) a jej obvod sa

Z

teda rovna n(r₁ + r₂). Z toho a z vysledkov ulohy 1 vyplyva:

Piast zrezaneho rotaćneho kuźela rovna sa sucinu stredneho rezu a strany.

Poznamka 3. Pre povrch zrezaneho rotaćneho kuźela — oznacime ho plsmenom P — uź 1’ahko odvodime vzorec

P = n[r\ + (?i + r₂)s + r\].

Cvicenih

1.    Vypocltajte priamo pouźitlm definlcie 1 ćl. 1. povrch rotaćneho valca.

2.    Ako sa zmenl a) piast, b) povrch rotaćneho valca, ak

1.    nasoblme jeho polomer clslom h.

2,    nasoblme jeho vyśku k,

3v nasoblme sućasne jeho povrch h a vysku k.

nasoblme polomer aj vyśku M [k, li su kladne clsla.)’

3.    Ako treba zmenit rozmery rotaćneho valca, aby jeho piast a) sa zdvojnasobil, b) zmenśil sa na desatinu póvodneho?

4.    Urćte a) presne, b) pribliźne medze pre ve!kost piasta a povrchu rotaćneho valca, ktoreho polomer podstavy r a vysku v sme zistili meranlm (pri meranl pripusfa sa chyba, która sa rovna e-nasobku meraneho rozmeru, |e| je vzhTadom na rozmery valca dost małe).

5.    Polomer r a vyska v rotaćneho valca zvacsil sa o kladnu hodnotu e. Ako sa zvaćśl jeho a) piast, b) povrch?

Aky je pribliźny prlrastok (pre dost małe e Yzhladom na rozmery valca), ked z ćlenov obsahujucich e uvaźujenie len tie, które ho obsahuju v prvej mocnine.

349