1954 Geometria 294

III. OBJEMY TELIES

. Uefimcia objemu

S niektórymi dóleżitymi telesami, hranolmi. iłilanmi (zrezanymi ihlanmi), valcami, kużelmi (zrezanymi kużelmi) a gulami (guIovym odsekom a gu!ovou vrstvou) sme sa oboznamili uż predtym. Hovorime im zakladne telesa.

Okrem tychto zakladnych telies budeme sa zaoberaf aj telesami,

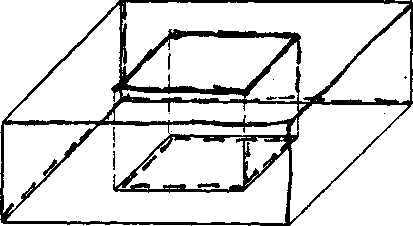
Obr. 52a

które możno zo zakladnych zlożit, t. j. budeme predpokladat, że toto te-leso możno rozlożit na niekolko (na konecny po-cet) navzajom sa nepre-nikajucich telies a każde teleso z tohto rozkładu je zakladnym telesom (obr. 52 a, b, c).

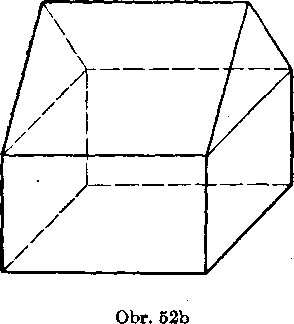
Pod navzajom nepre-nikajucimi sa telesami rozumienie take, pri których nijake teleso neobsahuje ynutorny bod dru-heho.

Podobne priberieme do uyahy eśte aj take telesa, które możno doplnit na zakladne telesa. Pritom vśak vy-żadujeme, aby yzniknute zakladnó teleso bolo możne rozlożit na niekoT-ko nayzajom sa neprenikajucich telies, z których jedno je prave dane teleso a każde zo zvyśujucich je zakladnym telesom (obr. 52a, obr. 53).

Każdemu obrazcu v rovine możno priradit kladne cislo, które sme nazya-li obsahom. Podobne możno dokazat, że aj pre telesa plati tyrdenie:

Każdemu z uvedenych telies możno priradit cislo s tymito vlast-nosfiami:

1.    Je kladne.

2.    Zhodnym telesam priradene cisla su rovnake.

3.    Ak sa teleso T składa z dvoch navzajom sa neprenikajucich telies T_1; T₂, rovna sa cislo priradene telesu T suctu ćisel priradenych telesam Tj a T₂.

Pre toto cislo zavedieme obyykle oznaeenie touto definiciou:

Definicia. Cislo, które możno podia predosleho tvrdenia priradif każdemu predtym uvedenemu telesu, nazveme objemom telesa.

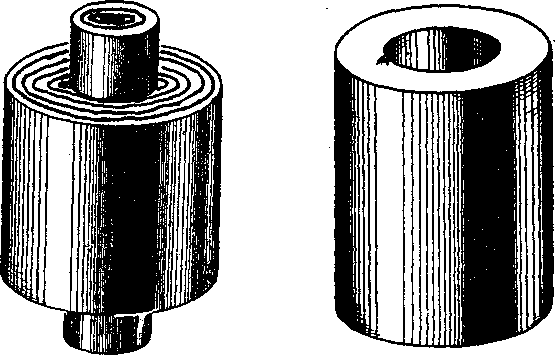
Obr. 52c    Obr. 53

Z tejto definicie a z naśho tvrdenia predovsetkym vyplyva:

Objem telesa ma tieto vlastnosti:

[1]    Objem telesa je kladne cislo.

[2]    Zhodne telesa, maju rovnake objemy.

[3]    Ak sa teleso T składa z dvoch telies T_x, T₂, które sa navzajom neprenikaju, potom objem telesa T rovna sa suctu objemov oboch telies T_x a T₂.

Poznamka 1. Tym sme vlastne formulovali vetu; dokazovat ju nebudeme. Yeta bovori v podstate len o existencii kladneho cisla (nazvali sme ho objem), które vyhovuje vlastnostiam [1], [2], [3]

295