1954 Geometria 218

v polrovine B[B^B₂. Tym je dokazane, że nase premiestenie prevedie

mnohouholnik £₁_B₂----B_n v mnohouholnik B{ B'₂.. .Bń\ obidva

mnohouholniky su teda zhodne.

Teraz móżeme pristupit k definicii velmi dóleżitej skupiny telies, totiż hranoloy.

Defini cia. Nech je dany hranoloyy priestor a dve navzajom rovno-beżne roviny a, r, które nie su jeho vrcholovymi rovinami. lJtvar spolocny hranolovemu priestoru a vrstve o, r nazyyame hranolom (obr. 74).

Prieseky rovin a, r hranoloyym priestorom nazyyame podstayami hranola, ich strany hranami podstayy a ich vrcholy vrcholmi hranola. Bocnymi hranami hranola sa volaju casti hran hranolovej płochy, a to

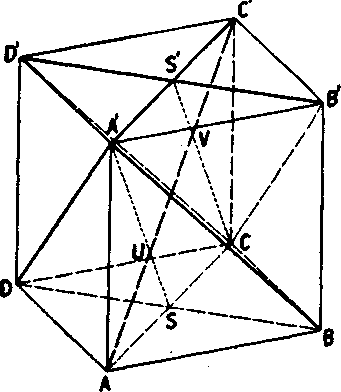
usecky, obmedzene vrcholmi na tychto hranach. Bocne steny su rovnobeżniky, leżiace v stenach prisluśnej hranolovej płochy. Podstayy a bocne steny tvoria povrch hranola. Body hranola, które neprisluchaju jeho povrchu, tvoria vnutro hranola. Ak yznikol hranol z n-bokćho hranoloveho priestoru, vola sa hranolom n-bo-kym.

Z definicie vidief, że n-boky hranol je obmedzeny dvoma zhodnymi n-uholnikmi an.rov-nobeżnikmi. Ma 2n vrcholov, 2n podstavnych a n bocnych hran.

Obr. 75    Vzdialenosf rovin podstay sa

vola yyśkou hranola.

Hranol sa nazyya kolmym hranolom, ak su jeho podstayy kolme na bocne hrany. Hranol, który nie je koimy, nazyva sa kosy.

Ak su podstayy kolmeho hranola pravidelne n-uholniky, vola sa hranol prayidelnym w-bokym hranolom.

Ak je riadiaci mnohouholnik rovnobeżnik, nazyya sa hranoloyy priestor rovnobeżnostenovy a hranol, który z neho yznikol, rovno-beżnosten,

Priklad 2. Je dany rovnobeżnosten ABCDA'B’C'D'.

a)    Dokażte, że roviny BDA', CB'D' delia telesoyu uhlopriecku AC na tri zhodne ćasti;

b)    Dokażte, że telesova uhlopriecka AG' prechadza tażiskom trojuholnika A'BD.

c)    Dokażte, że v pripade kocky je uhlopriecka AC kolma na roviny BDA’ a CB’D'.

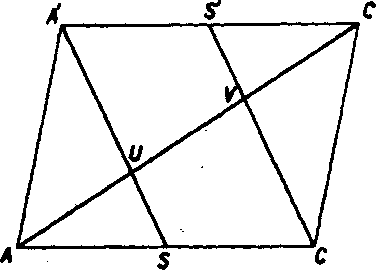
Riesenie: a) Prieseciky telesovej uhlopriecky AC s rovinami BDA' a CB'D' najdeme pomocou rovinv ACC (obr. 75), która pretina obi-dve roviny v priamkach A 'S a GS', kde S a<S”su stredy dolnej a hornej podstayy. Priese-ćiky oznacime U a V. Dokaż urobime najprehladnejśie na pomocnom obrazku (obr. 76), który je rysovany v rovine ACC. Z obrazka ihned’ yidief, że usecka SU je stredna priec-ka trojuholnika ACV, a teda AU = UV. Obdobne v troj-uholniku A'UC' ukażeme, że UV — VC, cim sme tvrdenie dokazali.

Obr. 76

b)    Z tych istych dvoch troj-uholnikovACVnA'UC, o których je zrejme, że su zhodne,

vyplyva ihned’ SU = ~A 'S. Na

O

obrazku 75 vśak yidiet, żeA'S je tażnica trojuholnika A'BI), cim je dpkazaneaj tvrdenie b).

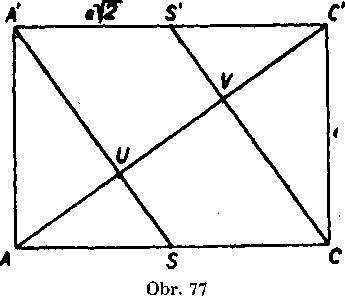
c)    V pripade kocky ukazuje situaciu v rovine ACC obr. 77.

Ak je a hrana kocky, je CC —

= a,AC — a]/2, C’S’ a ]j2_]

Jt

CC'

C'S' a Ann.

AOC

plati teda - _cc,

je podobny /\CC'S'. Z toho vyplyva, że CS' X AC a rovnako aj A 'S _L AC. Je zrejme, że pri kocke (alebo pri kvadri so śtvorcovou pod-stavou) jevżdy AC J^BD. Ztohoyyplyya: AC ±A'BD& AC ±CB'D'.

219