1954 Geometria 278

śujeme aj inym sposobom neż zdrójnasoboranim (napr. zvacsovamm poctu stran o jednu, obr. 31). Ani v tomto pripade nezależi na tom. z ktoreho n-uholnika rychadzame.

Mnohouholniky, które sme poużivali v dokaże, nemusia byt do-konca ani pravidelne. V tomto pripade rnusime rśak vyżadovat, aby

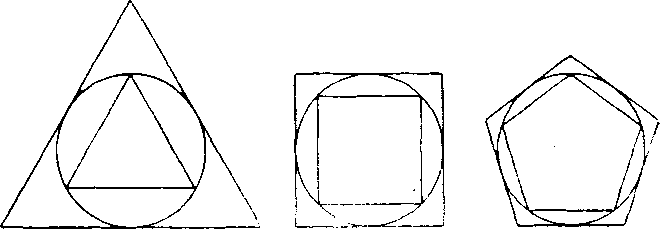
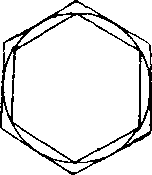
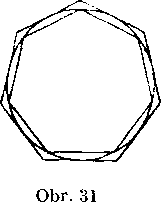
sa neobmedzenym zracSoranim poctu ich stran rolkosti rśetkych stran bllżili k nule. Tato podmienka je pri praridelnom mnohouholniku vżdy splnena, ako sme si to dokazali v cviceniach 2 a 4 na str. 267.

Veta 2. JYech SAB je rysek kruhu o polomere r (obr. 32). Yer-kosf uhla ASB nech sa rovna v stupnorej miere uhlu «. Potom obsah rys oku SAB je

360 ‘

Ked za jednotkory uhol zvolime stupeń, t. j. — praveho uhla,

PU

je x kladne cislo menśie neź 360.

Dokaż urobime v troch castiacb.

Dokażeme, że veta plati, ak 1) a je cele cislo, 2) a je racionalne cislo, 3) « je realne cislo.

1. Ak je a cele cislo, móżeme yysek SAB zlożit z a zhodnych vy-sekov, których uliol ma yelkost 1. Obsah każdeho z tychto jednotko-yych vysekov

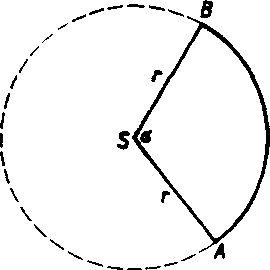
Obr. 32

P' =

nr²

360

(podia podmienky (2) a poznamky 2 k definicii obrazca). Preto obsah yyseku SAB

P = «.P' = A

nr²    Ti.r².a

360 ⁼    360

2. Nech uhol ASB ma racio-nalnu yelkost a. Potom a możno vyjadrii vo tvare ziomku:

m

A

m, n su cele cisla, n ^ 0. ZvoIme — stupńa ako novu jednotku uhla.

Tb

Vel’kost uhla ^ASB y tejto novej jednotke rovna sa celemu ćislu m. Podia prave dokazanej prvej casti vety obsah yyseku SAB rovna sa

P = m.P',

kde P' je obsah yyseku, ktoreho uhol ma v novej jednotke yelkost 1.

Tento uhol ma vel’kosf — uhloveho stupńa. Preto podrą podmienky [2]

‘n

a poznamky k definicii obsahu je

P' =

nr² 360 ii

Teda

_n    ,,,    nr² m nr² nr²x

£* — -m,    _ -— ___ _ — _

' 360 n n ' 360    360 ‘

3. Nech je yelkost uhla <yASB Tuboyolne realne cislo. Ako sme sa naućili pri dokaże vety 1 predoslej kapitoly (precitajte si poznamku str. 277), możno a vyjadrii ako spoloćny limit dvoch postupnosti.

279