1954 Geometria 140

Niektóre axiómy a vety o incidencii możno vyslovit aj v»dnej formę pomocou slovesa ,,urcovat“. Napy_ axióma I znie tak to ■. dvoma rożnymi bodmi je urćena jedina priamka.

Cvicenie

1.    Kolko różnych priamok je urcenych n różnymi bodmi, z których nijake tri neleźia na jednej priamke?

2.    Je dane n różnych bodov A_v A₂,. . ., A_n (n > 2). Body A_1; A₂, A₃ leżia na jednej priamke, nijake tri z danych hodov neleźia na jednej priamke. Kolko różnych priamok je urcene bodmi A_1; A₂,. .., A_n%

3.    Je dane n różnych bodov A_v A₂,A_n (n > 3). Body A_v A₂, A_s, A₄ leżia na jednej priamke a nijake tri z danych bodov okrem trojice A_v A₂, A₃; A_v A₂, A₄; A^A^A^; A₂, A₃, A_t neleźia na jednej, priamke. Kolko różnych priamok je urcene bodmi A_x, A₂,..., A_n%

4.    Vyslovte pomocou slovesa ,,urćovat“ axiómu III, IV a vetu 1 a 2.

5.    Je dane n różnych bodov A_v A₂, ..A_n(n >3). Body A_v A₂, A₃, A_i leżia v rovine; nijake tri z danych bodov neleźia na jednej priamke. Kolko różnych rovin je urcene bodmi A_v A₂,.... A_nl

6.    Vo dvoch różnych rovinach q, o' leżia trojuholniky ABC, A'B'C\ pre ne plati A = A', B = B', C = C'. iPriamky AA', BB', CC prechadzaju urcitym bodom F. Priamky AB, A'B' sa pretinaju v bodę C₀, priamky BC, B'C' v bodę A₀, priamky CA, C'A' v bodę

B₀.

Dokażte, że body A₀, B₀, C₀ leżia na jednej priamke.

7.    Najdite vhodne priklady z hmotneho sveta objasńujuce tvrdenie viet 1, 2.

2. Vzajomna poloha priamok a rovfn

Teraz sa budeme zaoberat yzajomnou polohou priamok a rovin v priestore. Pritom budeme zistovat predovsetkym ich spolocne body.

A. Dve roviny. Dve roviny bud’ splyvaju, bud’ su różne. Dve różne roviny bud’ nemaju spolocny bod, bud’ maju podia axiómy IV spolocnu priamku. Mimo tejto priamky uż nemaju spolocny bod. V tomto po-slednom pripade roviny sa nazyvaju róznobeżne, spolocna priamka ich priesecnieou. Dve splyvajuce roviny alebo dve roviny bez spolocńych bodov sa nazyvaju rovnobeżne. Rovnobeżnost rovin q, a zapisujeme q || a alebo a || q. Priesecnicu p rovin a, (} zapisujeme znakom p s

B.    Priamka a ronina. Ak neleżi priamka v rovine, ma s ńou podia axiómy II najviac jeden spolocny bod (t. j. jeden alebo ani jeden). Ak maju priamka a rovina jediny spolocny bod, nazyyaju sa rOzno-beżne, spolocny bod ich priesecikom. V ostatnych pripadoch, t. j. ak leżi priamka v rovine, alebo ak nemaju priamka a rovina spolocny bod, hovorime, że su roynobeźne. Rovnobeżnost priamky p s rovinou q zapisujeme p || g alebo q || p. Priesecik Q priamky m s rovinou r zapisujeme znakom Q = m.r.

C.    Dve priamky. Dve różne priamky, które maju jediny spolocny bod, leżia podia vcty 2 v urcitej rovine. Take dve priamky sa nazyyaju rdznobeźky, spolocny bod je ich priesecik. I)ve różne priamky bez społocneho bodu bud' leżia v tejże rovine a nazyyaju sa roynobeżky, bud obe neleźia v nijake j royine a nazyyaju sa mimobeźky. Splyyajuce priamky tież pocitame medzi roynobeżky. Rov-nobeżnost priamok a, b zapisujeme a 11 b alebo b 11 a. Priesecik R rózno-beżiek u, v zapisujeme znakom B = u. v.

Pri yyklade o rovno-beżkach v planimetrii yychadzali sme zo slay-nej axiómy, zvanej piaty Euklidov postulat.

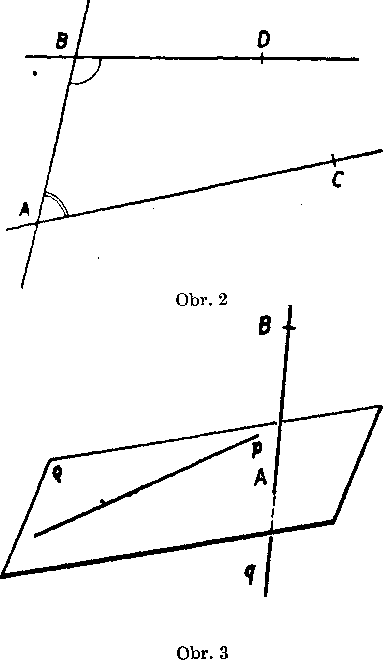
AxiómaV. Ak su vro-yine dane dva prilahle uhly <^c ABD, BAG (obr. 2), których sucet je uhol duty, potom polpriam-ky AG, BD maju spoloc-ny bod (pretmaju sa).

V planimetrii sme pred-pokladali, że tato axióma plati pre urcitu royinu, yktorej leżiavśetkyutva-ry. V stereometrii pred-pokladame, że tato axió-ma plati pre każdu royinu.

Preto budu mat utvary

141