1954 Geometria 142

każdej roviny nsetky vlastnosti, które możno odnodit z axiómy I aż V. Napr. pre każdu rovinu budę platit veta:

Ak su a, b dve różne ronnobeżky roviny q, a ak je c priamka roviny q róznobeżna s priamkou a, priamka c je róznobeżna aj s priamkou b.

Tuto vetu poużijeme pri diskusii nzajomnej polohy troch rovin.

Teraz dokażeme existen-ciu mimobeżiek.

Obr. 4a

Znolime l’ubovoIne priam-ku p a mimo nej bod A. Priamkou p a bodom A pre-chadza jedina ronina q (obr. 3). Mimo roviny q znolime bod B; potom priamky p. q = AB su mimobeżne; pre-toże każda ronina, która by obsahonala priamky p, q, musela by obsahonaf priam-ku p aj bod,A.Taka rovina je nśak iba jedna a je to ro-vina o; ronina o nsak neob-sahuje bod B.ja teda neobsa-huje ani priamku q.

V predchadzajiicej unahe sme sa pokusili zdanlino bez akehokolnek odnolania sa na nazor, iba z axiómy, dokazat, że existuju mimobeżky. No ńnaha nebola dokonała. Po-vedali sme; Znolme si priamku, mimo nej bod, potom dalsi bod mimo roviny. Alfe możnost takycb nolieb nijako nenyplyna z axióm, leż iba z nazoru. Tento rozbor sme uniedli preto, aby sme ukazali, że naśe śtyri axiómy-netvoria uplnu zakladńu pre odvodzovanie viet o incidencii bodov, pri amok a ronin. Skutocne teda pri prisne vedeckej vystanbe geometrie je nenyhnutne nychadzat z yacśieho poctu axióm incidencie. My sme sa nśak n naśom nyklade obmedziii iba na ukażku niektórych axióm a aj dalej si budeme poci-naf podobne. Nebudeme preto nikdy (vrdif, że sme v 10. roeniku pre-viedli axiomaticku vystavbu stereometrie.

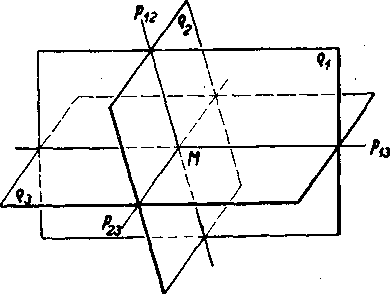
D. Tri roviny. Majme tri różne roviny q_v q₂, g₃. Bud’ su każde dve z nich rovnobeżne (bbr. 4a), bud’ su niektóre dve, napr. q_x, q₂ rózno-beżne; ich priesecnicu oznacime p₁₂. Priamka p₁₂ może mat vzhl'adoiu na rovinu o₃ trojaku vza-jomnu polohu.

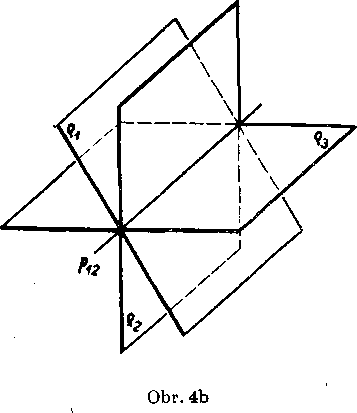
(1)    Priamka p_1>2 leżi v g₃;roviny q_v o₂, p₃obsahu-ju potom spoloćnu priam-ku (obr. 4b).

(2)    (Obr. 4c.) Priamka Pi,2 P^retina p₃ v bodę M; tento bod je potom spoloc-ny vsetkym trom rovi-nam. Każde dve z nich su róznobeżne a vśetky tri prieseenice p₁₂, p₂₂, p_3>iprechadzaju bodom df.

(3)    Priamka p_1;2 nema

s rovinou ą₃ spoioony bod.    Obr. 4c

Potom su dve możnosti:

Bud’ je rovina'g₃ róznobeżna s rovinou aj s rovinou q₂ a każde dve z priesecnic p₁₂, p_2>s, p_us su navzajom rovnobeżne (obr. 4d). Skutoćne,

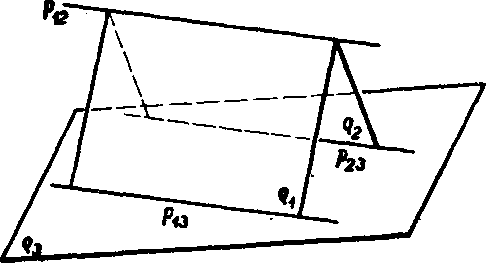
Obr. 4d

143