1954 Geometria 318

ich limitoyanim najdeme

lim Vń ^ V, V ś lim V„.

n-> co    n-» oo

Pretoze sa vsak lim Vń = pv a sucasne lim V'ń — pv, vyplyva n->co    n->00

z toho, że V = pv, ako sme mali dokazaf.

Poznamka. Ak sa polomer rotacneho valca rovna r, potom pre obsah p jeho podstayy plati, ako vieme, p = nr², a teda objem V rotacneho valca je dany vzorcom

V = nr²v.

V praxi sa okrem valca yyskytuju aj jeho casti, z których najdóle-żitejśie su vysek valca a odsek valca.

Vysek valca (obr. 70) je cast valca obmedzena klinom, ktoreho hrana leżi y osi valca; odsek valca (obr. 71) je casf valca obmedzena rovinou roynobeżnou s osou valca ,a yzdialenou od nej menej neż polomer yalca. Pocitame ich tież medzi zakladne telesa (pozri str. 294). Niekedy sa javi yyhodnym nazyyat tieto casti jednoducho valec a pripojif udaj o podstave; v prvom pripade (obr. 70) hovorime o valci, ktoreho pod-stavou je yysek kruhu, v druhom pripade (obr. 71) o valci, ktoreho podstayou je kruhovy odsek.

Że aj pre tieto valce plati tvrdenie vety 1, możno dokazat metódou poużitou pri dokazovani vety 1.

Pre objem rotacneho kużela plati veta, która je obdobna vete 5 pre objem ihlana.

Veta 6. Objem rotacneho kużela rorna sa tretine su&inu obsabn poi-stayy a yelkosti vysky.

Postup dókazu je podobny tomu, który sme poużili pre urcenie ob-jemu ihlana. Nebudeme ho opakovat.

Ak ma podstava kużela polomer r, potom obsah podstayy je p = nr², a teda pre objem V kużela s yyśkou v dostavame vzorec

V — nr² v.

u

tJloha 1. TJrcte objem zrezaneho rotacneho kużela.

V

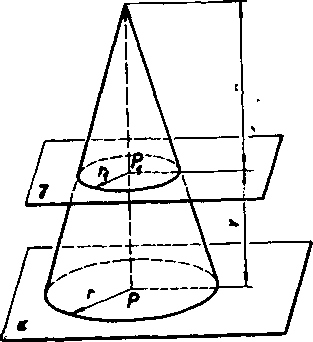
Rieśenie (obr. 72). Nech r_} je polomer podstayy kużela, który dopina dany zrezany kużel na piny kużel; vyśku dopliiujuceho kużela oznac-me x. Ak je r polomer druhej podstayy zrezaneho kużela (nevyhnutne r >r_x), potom vyśka kużela, na który sme zrezany kużel doplnili, rov-na sa v -|- x.

Z podobnosti trojuholnikoy, v których IubovoIna rovina prechadzajuca osou zrezaneho kużela pretina obidva rotacne kużele, vyply va

r : r_x = (a: -f- v) : x,

z toho dostaneme (yzhladom na to, żer — r_x > 0)

x =    (1)    Obr. 72

r—r_x    '

Podia vlastnosti [3] je objem zrezaneho rotacneho kużela (oznacme ho F) rozdielom objemov obidyoch rotacnych kużeloy, teda

V = — nr² (v -f x) — nr\x = ^-n [r² v Ą- {r² — rf)x];

o    o    O

319