1954 Geometria 328

Celkom podobne najdeme

lim F₂ = -i ng² v -j- ~ nv⁸.

łl->O0    ^    o

Oba limity sa teda navzajom rovnaju.

Z nerovnosti (2) vidno, że objem F nemóże byt vacśi,neż je lim V_x ^k    »->oó

a sucasne nemóże byt mensi neż lim F₂. Pretoże sa vśak podia pre-

łt-J-CO

dośleho Wkładu oba limity navzajom rovnaju, musi sa objem uvażo-vaneho odseku rovnat tomuto spolocnemu limitu, t. j. musi byt

F=— ng²v + ~ nu³.    (3)

Teraz uż móżeme urcit objem gule. Rovina prechadzajuca stredom gule rozdeluje ju na dve zhodne polgule, teda objem gule rovna sa podrą vlastnosti [3] dvojnasobku objemu polgule. Polgula je vsak odsek s vyskou v — r\ polomer g jej podstavy rovna sa tież r a objem

polgule sa podia (3) rovna ~

nr

.3 _

nr

Z toho ihned

vyplyva, że objem gule rovna sa — nr³, co sme mali dokazat.

'Oloha 1. Urcte objem gul'oveho odseku.

Rieśenie. Ak je r polomer prisluśnej gule, g polomer podstavy odseku, v vyśka odseku a F jeho objem, objem odseku pre v ^ r rovna 11

sa — ng²v + — nu³, ako sme dokazali v predoślom dokaże [pozri (3)].

a    O

.Ak je vyśka odseku v > r (pricom vsak v < 2r), TŚimneme si okiem daneho odseku eśte odsek, który dopina prvy odsek na gulu o polo-mere r. Podia vlastnosti [3] objem daneho odseku rovna sa rozdielu objemu gule a doplńujuceho odseku. Pretoże vyśka doplnujuceho odseku je 2r — v, teda mensia neż r, plati pre jeho objem uż dokazany vzorec. Ak hladany objem daneho odseku oznaćime F, dostaneme

F =

nr

[y ⁿ i^2>' — v)q² + j n (^{2r v})^s ]

= — nrg² -f ~ nvg² -f- 2nr²v —- nrv² nu³

£    O

= nr [r(2r — v) — 2²] + ^ nug² -f nu³.

Pre q² vśak (ked’ pouźijeme Euklidovu vetu pre urcenie vysky pravó-uhlóho trojuholnika) piat! p² = v(2r — v), a tak aj v tomto prlpade objem odseku

V — 7- 7tvp² + \r nv³.

2    o

Poznamka. Z yysledku vyplyva, że objem odseku rovna sa suctu objemu yalca, ktoreho podstava rovna sa podstare odseku a vyśka

1 odsek    2 gida

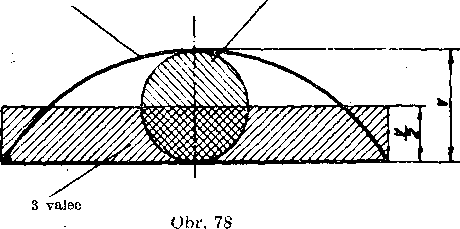
rovna sa polovici vyśky odseku a objemu gule, której polomer rovna sa polovici vysky daneho odseku (obr. 78).

"Ol oh a 2. Urcte objem gul'ovej vrstvy.

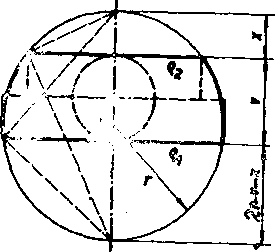
Obr. 79

Ii i e sonie. Nech je dana vrstva vyseknuta z gule o polomere r a nech su polomery podstav vrstvy o_1; g₂ a vyska vrstvy nech je ,v. Danu vrstvu doplńme takym gul’ovym odsekom, który neobsahuje vrstvu, ale społu s iiou tvorl gul’ovy odsek o polomere podstavy p_x (obr. 79).

Polomer pod. tn vy doplńujueeho gu-l’oveho odseku nech je o₂; jej vyska nech je x, vyśka vzńiknuteho odseku je v x. Objem dar ej guIovej vrstvy oznaeme V, objem vzniknu-teho guloreho odseku F, a objem doplńujueeho gu!oveho odseku V₂.

Podia ylastnosti [3]

v==v_x~v_t,

a teda ak pouźijeme vysledok ulo-

hyi,